編者按:回歸其實(shí)就是對(duì)已知公式的未知參數(shù)進(jìn)行估計(jì),Logistic regression是線性回歸的一種,是機(jī)器學(xué)習(xí)中十分常用的一種分類算法,在互聯(lián)網(wǎng)領(lǐng)域得到了廣泛的應(yīng)用。本文來(lái)自騰訊馮揚(yáng)的博客:并行邏輯回歸 ,主要從并行化的角度討論LR的實(shí)現(xiàn)。
CSDN推薦:歡迎免費(fèi)訂閱《Hadoop與大數(shù)據(jù)周刊》獲取更多Hadoop技術(shù)文獻(xiàn)、大數(shù)據(jù)技術(shù)分析、企業(yè)實(shí)戰(zhàn)經(jīng)驗(yàn),生態(tài)圈發(fā)展趨勢(shì)。 以下為原文: 邏輯回歸(Logistic Regression,簡(jiǎn)稱LR)是機(jī)器學(xué)習(xí)中十分常用的一種分類算法,在互聯(lián)網(wǎng)領(lǐng)域得到了廣泛的應(yīng)用,無(wú)論是在廣告系統(tǒng)中進(jìn)行CTR預(yù)估,推薦系統(tǒng)中的預(yù)估轉(zhuǎn)換率,反垃圾系統(tǒng)中的識(shí)別垃圾內(nèi)容……都可以看到它的身影。LR以其簡(jiǎn)單的原理和應(yīng)用的普適性受到了廣大應(yīng)用者的青睞。實(shí)際情況中,由于受到單機(jī)處理能力和效率的限制,在利用大規(guī)模樣本數(shù)據(jù)進(jìn)行訓(xùn)練的時(shí)候往往需要將求解LR問(wèn)題的過(guò)程進(jìn)行并行化,本文從并行化的角度討論LR的實(shí)現(xiàn)。
1. LR的基本原理和求解方法
LR模型中,通過(guò)特征權(quán)重向量對(duì)特征向量的不同維度上的取值進(jìn)行加權(quán),并用邏輯函數(shù)將其壓縮到0~1的范圍,作為該樣本為正樣本的概率。邏輯函數(shù)為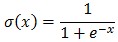 ,曲線如圖1。
,曲線如圖1。
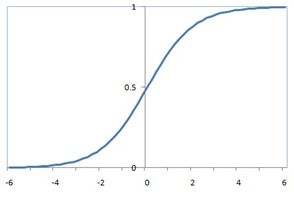
圖1 邏輯函數(shù)曲線
給定M個(gè)訓(xùn)練樣本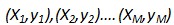 ,其中Xj={xji|i=1,2,…N} 為N維的實(shí)數(shù)向量(特征向量,本文中所有向量不作說(shuō)明都為列向量);yj取值為+1或-1,為分類標(biāo)簽,+1表示樣本為正樣本,-1表示樣本為負(fù)樣本。在LR模型中,第j個(gè)樣本為正樣本的概率是:
,其中Xj={xji|i=1,2,…N} 為N維的實(shí)數(shù)向量(特征向量,本文中所有向量不作說(shuō)明都為列向量);yj取值為+1或-1,為分類標(biāo)簽,+1表示樣本為正樣本,-1表示樣本為負(fù)樣本。在LR模型中,第j個(gè)樣本為正樣本的概率是:
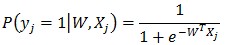
其中W是N維的特征權(quán)重向量,也就是LR問(wèn)題中要求解的模型參數(shù)。
求解LR問(wèn)題,就是尋找一個(gè)合適的特征權(quán)重向量W,使得對(duì)于訓(xùn)練集里面的正樣本,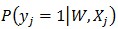 值盡量大;對(duì)于訓(xùn)練集里面的負(fù)樣本,這個(gè)值盡量小(或
值盡量大;對(duì)于訓(xùn)練集里面的負(fù)樣本,這個(gè)值盡量小(或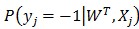
盡量大)。用聯(lián)合概率來(lái)表示:
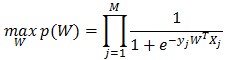
對(duì)上式求log并取負(fù)號(hào),則等價(jià)于:
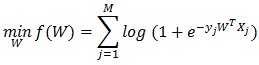 公式(1)
公式(1)
公式(1)就是LR求解的目標(biāo)函數(shù)。
尋找合適的W令目標(biāo)函數(shù)f(W)最小,是一個(gè)無(wú)約束最優(yōu)化問(wèn)題,解決這個(gè)問(wèn)題的通用做法是隨機(jī)給定一個(gè)初始的W0,通過(guò)迭代,在每次迭代中計(jì)算目標(biāo)函數(shù)的下降方向并更新W,直到目標(biāo)函數(shù)穩(wěn)定在最小的點(diǎn)。如圖2所示。

圖2 求解最優(yōu)化目標(biāo)函數(shù)的基本步驟
不同的優(yōu)化算法的區(qū)別就在于目標(biāo)函數(shù)下降方向Dt的計(jì)算。下降方向是通過(guò)對(duì)目標(biāo)函數(shù)在當(dāng)前的W下求一階倒數(shù)(梯度,Gradient)和求二階導(dǎo)數(shù)(海森矩陣,Hessian Matrix)得到。常見(jiàn)的算法有梯度下降法、牛頓法、擬牛頓法。
(1) 梯度下降法(Gradient Descent)
梯度下降法直接采用目標(biāo)函數(shù)在當(dāng)前W的梯度的反方向作為下降方向: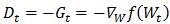
其中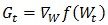 為目標(biāo)函數(shù)的梯度,計(jì)算方法為:
為目標(biāo)函數(shù)的梯度,計(jì)算方法為:
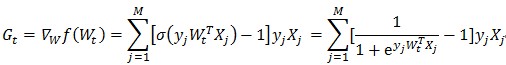 公式(2)
公式(2)
(2) 牛頓法(Newton Methods)
牛頓法是在當(dāng)前W下,利用二次泰勒展開(kāi)近似目標(biāo)函數(shù),然后利用該近似函數(shù)來(lái)求解目標(biāo)函數(shù)的下降方向: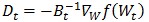 。其中Bt為目標(biāo)函數(shù)f(W)在Wt處的海森矩陣。這個(gè)搜索方向也稱作牛頓方向。
。其中Bt為目標(biāo)函數(shù)f(W)在Wt處的海森矩陣。這個(gè)搜索方向也稱作牛頓方向。
(3) 擬牛頓法(Quasi-Newton Methods):
擬牛頓法只要求每一步迭代中計(jì)算目標(biāo)函數(shù)的梯度,通過(guò)擬合的方式找到一個(gè)近似的海森矩陣用于計(jì)算牛頓方向。最早的擬牛頓法是DFP(1959年由W. C. Davidon提出,并由R. Fletcher和M. J. D. Powell進(jìn)行完善)。DFP繼承了牛頓法收斂速度快的優(yōu)點(diǎn),并且避免了牛頓法中每次迭代都需要重新計(jì)算海森矩陣的問(wèn)題,只需要利用梯度更新上一次迭代得到的海森矩陣,但缺點(diǎn)是每次迭代中都需要計(jì)算海森矩陣的逆,才能得到牛頓方向。
BFGS是由C. G. Broyden, R. Fletcher, D. Goldfarb和D. F. Shanno各自獨(dú)立發(fā)明的一種方法,只需要增量計(jì)算海森矩陣的逆Ht=Bt-1,避免了每次迭代中的矩陣求逆運(yùn)算。BFGS中牛頓方向表示為:
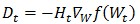
L-BFGS(Limited-memory BFGS)則是解決了BFGS中每次迭代后都需要保存N*N階海森逆矩陣的問(wèn)題,只需要保存每次迭代的兩組向量和一組標(biāo)量即可:
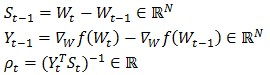
在L-BFGS的第t次迭代中,只需要兩步循環(huán)既可以增量計(jì)算牛頓方向:
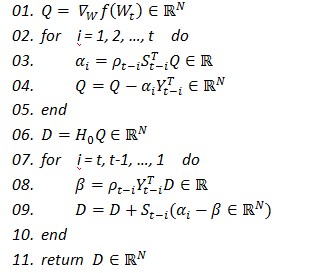
2. 并行LR的實(shí)現(xiàn)
由邏輯回歸問(wèn)題的求解方法中可以看出,無(wú)論是梯度下降法、牛頓法、擬牛頓法,計(jì)算梯度都是其最基本的步驟,并且L-BFGS通過(guò)兩步循環(huán)計(jì)算牛頓方向的方法,避免了計(jì)算海森矩陣。因此邏輯回歸的并行化最主要的就是對(duì)目標(biāo)函數(shù)梯度計(jì)算的并行化。從公式(2)中可以看出,目標(biāo)函數(shù)的梯度向量計(jì)算中只需要進(jìn)行向量間的點(diǎn)乘和相加,可以很容易將每個(gè)迭代過(guò)程拆分成相互獨(dú)立的計(jì)算步驟,由不同的節(jié)點(diǎn)進(jìn)行獨(dú)立計(jì)算,然后歸并計(jì)算結(jié)果。
將M個(gè)樣本的標(biāo)簽構(gòu)成一個(gè)M維的標(biāo)簽向量,M個(gè)N維特征向量構(gòu)成一個(gè)M*N的樣本矩陣,如圖3所示。其中特征矩陣每一行為一個(gè)特征向量(M行),列為特征維度(N列)。
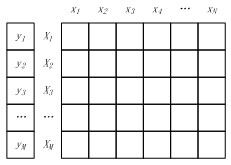
圖3 樣本標(biāo)簽向量 & 特征向量
如果將樣本矩陣按行劃分,將樣本特征向量分布到不同的計(jì)算節(jié)點(diǎn),由各計(jì)算節(jié)點(diǎn)完成自己所負(fù)責(zé)樣本的點(diǎn)乘與求和計(jì)算,然后將計(jì)算結(jié)果進(jìn)行歸并,則實(shí)現(xiàn)了“按行并行的LR”。按行并行的LR解決了樣本數(shù)量的問(wèn)題,但是實(shí)際情況中會(huì)存在針對(duì)高維特征向量進(jìn)行邏輯回歸的場(chǎng)景(如廣告系統(tǒng)中的特征維度高達(dá)上億),僅僅按行進(jìn)行并行處理,無(wú)法滿足這類場(chǎng)景的需求,因此還需要按列將高維的特征向量拆分成若干小的向量進(jìn)行求解。
(1) 數(shù)據(jù)分割
假設(shè)所有計(jì)算節(jié)點(diǎn)排列成m行n列(m*n個(gè)計(jì)算節(jié)點(diǎn)),按行將樣本進(jìn)行劃分,每個(gè)計(jì)算節(jié)點(diǎn)分配M/m個(gè)樣本特征向量和分類標(biāo)簽;按列對(duì)特征向量進(jìn)行切分,每個(gè)節(jié)點(diǎn)上的特征向量分配N/n維特征。如圖4所示,同一樣本的特征對(duì)應(yīng)節(jié)點(diǎn)的行號(hào)相同,不同樣本相同維度的特征對(duì)應(yīng)節(jié)點(diǎn)的列號(hào)相同。
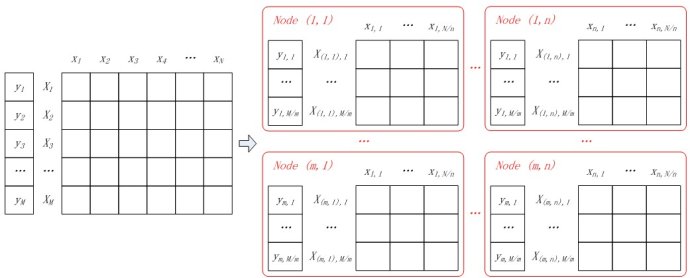
圖4 并行LR中的數(shù)據(jù)分割
一個(gè)樣本的特征向量被拆分到同一行不同列的節(jié)點(diǎn)中,即: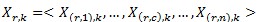
其中Xr,k表示第r行的第k個(gè)向量,X(r,c),k表示Xr,k在第c列節(jié)點(diǎn)上的分量。同樣的,用Wc表示特征向量W在第c列節(jié)點(diǎn)上的分量,即: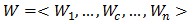
(2) 并行計(jì)算
觀察目標(biāo)函數(shù)的梯度計(jì)算公式(公式(2)),其依賴于兩個(gè)計(jì)算結(jié)果:特征權(quán)重向量Wt和特征向量Xj的點(diǎn)乘,標(biāo)量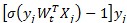 和特征向量Xj的相乘。可以將目標(biāo)函數(shù)的梯度計(jì)算分成兩個(gè)并行化計(jì)算步驟和兩個(gè)結(jié)果歸并步驟:
和特征向量Xj的相乘。可以將目標(biāo)函數(shù)的梯度計(jì)算分成兩個(gè)并行化計(jì)算步驟和兩個(gè)結(jié)果歸并步驟:
① 各節(jié)點(diǎn)并行計(jì)算點(diǎn)乘,計(jì)算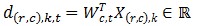 ,其中k=1,2,…,M/m,
,其中k=1,2,…,M/m,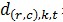 表示第t次迭代中節(jié)點(diǎn)(r,c)上的第k個(gè)特征向量與特征權(quán)重分量的點(diǎn)乘,Wc,t為第t次迭代中特征權(quán)重向量在第c列節(jié)點(diǎn)上的分量。
表示第t次迭代中節(jié)點(diǎn)(r,c)上的第k個(gè)特征向量與特征權(quán)重分量的點(diǎn)乘,Wc,t為第t次迭代中特征權(quán)重向量在第c列節(jié)點(diǎn)上的分量。
②對(duì)行號(hào)相同的節(jié)點(diǎn)歸并點(diǎn)乘結(jié)果:
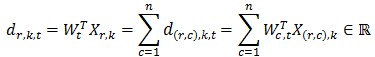
計(jì)算得到的點(diǎn)乘結(jié)果需要返回到該行所有計(jì)算節(jié)點(diǎn)中,如圖5所示。
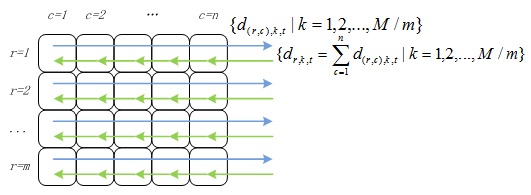
圖5 點(diǎn)乘結(jié)果歸并
③ 各節(jié)點(diǎn)獨(dú)立算標(biāo)量與特征向量相乘:
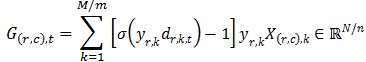
G(r,c),t可以理解為由第r行節(jié)點(diǎn)上部分樣本計(jì)算出的目標(biāo)函數(shù)梯度向量在第c列節(jié)點(diǎn)上的分量。
④ 對(duì)列號(hào)相同的節(jié)點(diǎn)進(jìn)行歸并:
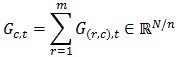
Gc,t就是目標(biāo)函數(shù)的梯度向量Gt在第c列節(jié)點(diǎn)上的分量,對(duì)其進(jìn)行歸并得到目標(biāo)函數(shù)的梯度向量:
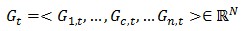
這個(gè)過(guò)程如圖6所示。
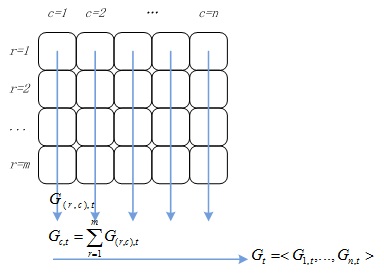
圖6 梯度計(jì)算結(jié)果歸并
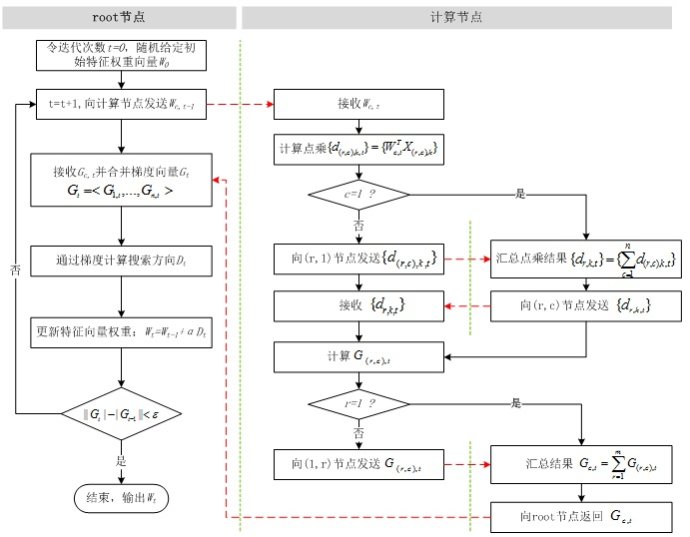
綜合上述步驟,并行LR的計(jì)算流程如圖7所示。比較圖1和圖7,并行LR實(shí)際上就是在求解損失函數(shù)最優(yōu)解的過(guò)程中,針對(duì)尋找損失函數(shù)下降方向中的梯度方向計(jì)算作了并行化處理,而在利用梯度確定下降方向的過(guò)程中也可以采用并行化(如L-BFGS中的兩步循環(huán)法求牛頓方向)。
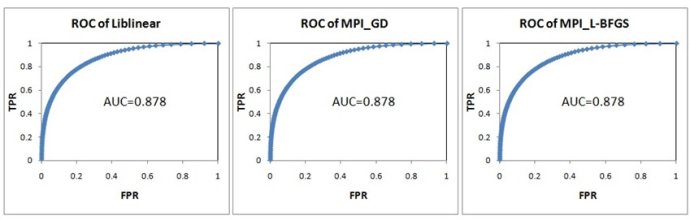
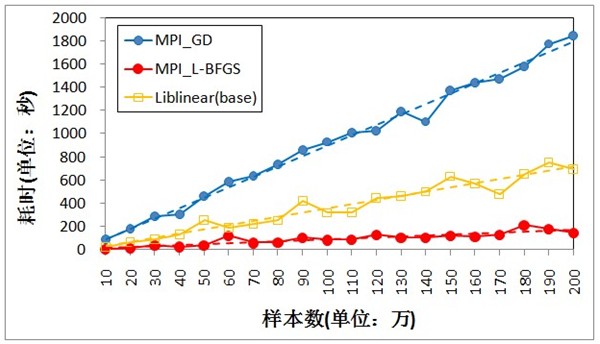
利用MPI,分別基于梯度下降法(MPI_GD)和L-BFGS(MPI_L-BFGS)實(shí)現(xiàn)并行LR,以Liblinear為基準(zhǔn),比較三種方法的訓(xùn)練效率。Liblinear是一個(gè)開(kāi)源庫(kù),其中包括了基于TRON的LR(Liblinear的開(kāi)發(fā)者Chih-Jen Lin于1999年創(chuàng)建了TRON方法,并且在論文中展示單機(jī)情況下TRON比L-BFGS效率更高)。由于Liblinear并沒(méi)有實(shí)現(xiàn)并行化(事實(shí)上是可以加以改造的),實(shí)驗(yàn)在單機(jī)上進(jìn)行,MPI_GD和MPI_L-BFGS均采用10個(gè)進(jìn)程。
實(shí)驗(yàn)數(shù)據(jù)是200萬(wàn)條訓(xùn)練樣本,特征向量的維度為2000,正負(fù)樣本的比例為3:7。采用十折交叉法比較MPI_GD、MPI_L-BFGS以及Liblinear的分類效果。結(jié)果如圖8所示,三者幾乎沒(méi)有區(qū)別。