卡爾曼濾波器是1種利用線性系統狀態方程,通過系統輸入輸出觀測數據,對系統狀態進行最優估計的算法。而且由于觀測包括系統的噪聲和干擾的影響,所以最優估計也可看作是濾波進程。
卡爾曼濾波器的核心內容就是5條公式,計算簡單快速,合適用于少許數據的預測和估計。
下面我們用1個例子來講明1下卡爾曼算法的利用。
假定我們想在有1輛小車,在 t 時刻其速度為 Vt ,位置坐標為 Pt,ut 表示 t 時刻的加速度,那末我們可以用Xt表示 t 時刻的狀態,以下:
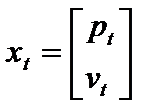
則我們可以得到,由t⑴ 時刻到 t 時刻,位置和速度的轉換以下:
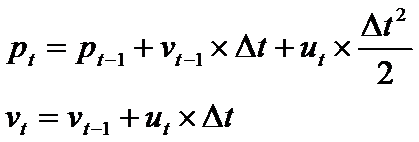
用向量表示上述轉換進程,以下:
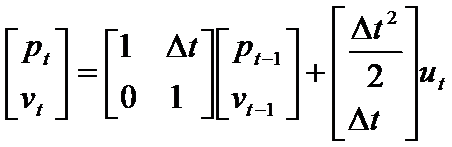
以下圖:
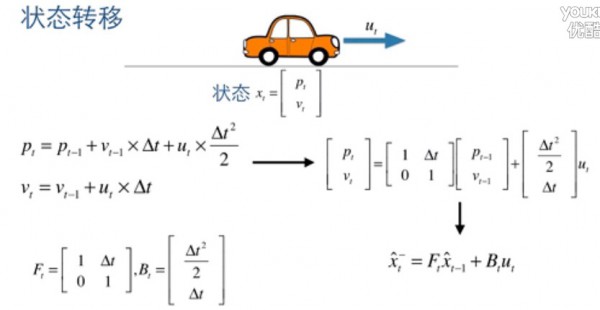
那末我們可以得到以下的狀態轉移公式:
其中矩陣 F 為狀態轉移矩陣,表示如何從上1狀態來推測當前時刻的狀態,B 為控制矩陣,表示控制量u如何作用于當前矩陣,上面的公式 x 有頂帽子,表示只是估計值,其實不是最優的。
有了狀態轉移公式就能夠用來推測當前的狀態,但是所有的推測都是包括噪聲的,噪聲越大,不肯定越大,協方差矩陣用來表示這次推測帶來的不肯定性
假定我們有1個1維的數據,這個數據每次丈量都不同,我們假定服從高斯散布,那末我們可以用均值和方差來表示該數據集,我們將該1維數據集投影到坐標軸上,以下圖:
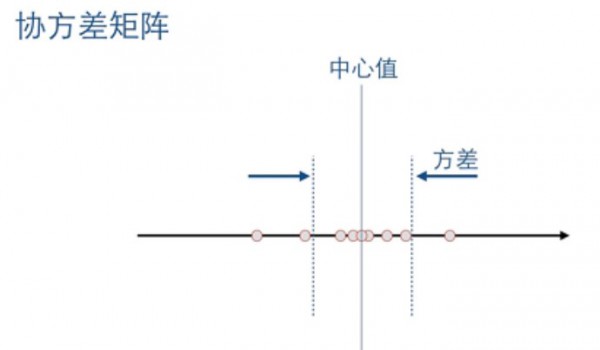
可以看到,服從高斯散布的1維數據大部份散布在均值附近。
現在我們來看看服從高斯散布的2維數據投影到坐標軸的情況,以下圖:
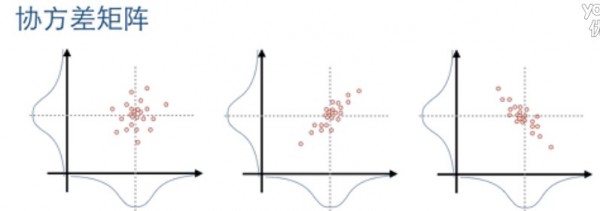
2維數據比1維數據略微復雜1點,投影后有3種情況,分別是:
左圖:兩個維的數據互不相干;
中圖:兩個維的數據正相干,也就是 y 隨著 x 的增大而增大(假定兩個維分別為 x 和 y)
右圖:兩個維的數據負相干,也就是 y 隨著 x 的增大而減小。
那怎樣來表示兩個維的數據的相干性呢?答案就是協方差矩陣。
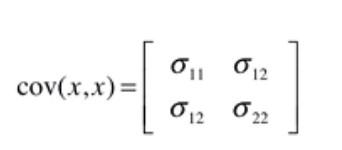
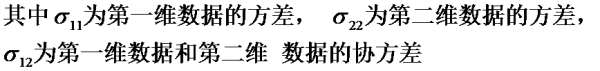
在公式(1)當中,我們已得到了狀態的轉移公式,但是由上面可知,2維數據的協方差矩陣對描寫數據的特點是很重要的,那末我們應當如何更新或說傳遞我們的2維數據的協方差矩陣呢?假設我們用 P 來表示狀態協方差,即
那末加入狀態轉換矩陣 F ,得到
也即:

因此我們便得到了協方差的轉換公式。
現在我們得到了兩個公式,應用這兩個公式能夠對現在狀態進行預測。依照我們的正常思路來理解,預測結果不1定會對嘛,肯定有誤差。而且在我們大多數回歸算法或是擬合算法中,1般思路都是先預測,然后看看這個預測結果跟實際結果的誤差有多大,再根據這個誤差來調劑預測函數的參數,不斷迭代調劑參數直到預測誤差小于1定的閾值。
卡爾曼算法的迭代思想也類似,不過這里根據誤差調劑的是狀態 X 。
在這里,我們的實際數據就是 Z, 以下圖:
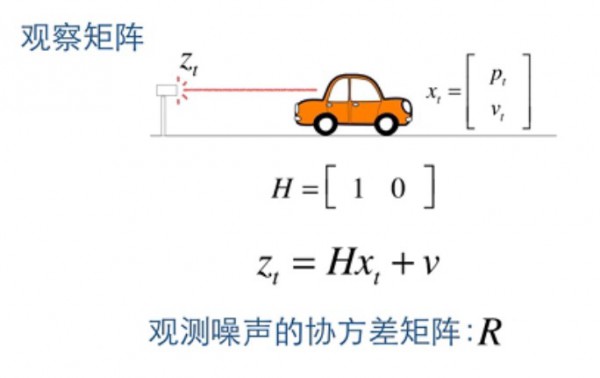
其中,矩陣 H 為丈量系統的參數,即視察矩陣,v 為觀測噪聲, 其協方差矩陣為R
那末我們的狀態更新公式以下:
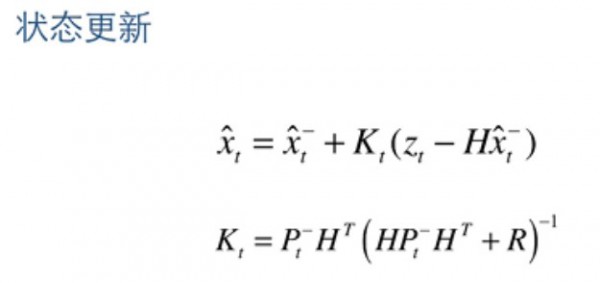
其中K 為卡爾曼系數, Z-Hx 則為殘差,也就是我們說的,預測值與實際值的誤差。
K的作用:
1.K 權衡預測協方差P和視察協方差矩陣R那個更加重要,相信預測,殘差的權重小,相信視察,殘差權重大,由 K 的表達是可以退出這個結論
2,將殘差的表現情勢從視察域轉換到狀態域(殘差與1個標量,通過K 轉換為向量),由 狀態 X 的更新公式可得到該結論。
至此,我們已得到了 t 狀態下的最優估計值 Xt。但為了能讓我們的迭代算法延續下去,我們還必須更新狀態協方差的值。

以上就是卡爾曼濾波算法的思想,只有簡單的 5 條公式,總結以下:
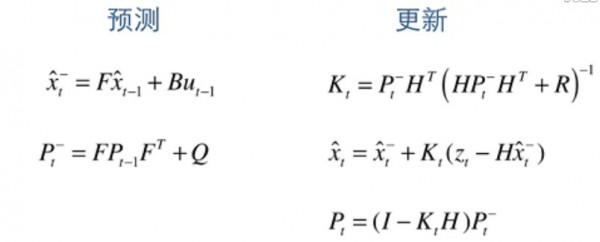
function kalmanFiltering
%%
clc
close all
%%
%
% Description : kalmanFiltering
% Author : Liulongpo
% Time:2015⑷⑵9 16:42:34
%
%%
Z=(1:2:200); %觀測值 汽車的位置 也就是我們要修改的量
noise=randn(1,100); %方差為1的高斯噪聲
Z=Z+noise;
X=[0 ; 0 ]; %初始狀態
P=[1 0;0 1]; %狀態協方差矩陣
F=[1 1;0 1]; %狀態轉移矩陣
Q=[0.0001,0;0 , 0.0001]; %狀態轉移協方差矩陣
H=[1,0]; %觀測矩陣
R=1; %觀測噪聲方差
figure;
hold on;
for i = 1:100
%基于上1狀態預測當前狀態
X_ = F*X;
% 更新協方差 Q系統進程的協方差 這兩個公式是對系統的預測
P_ = F*P*F'+Q;
% 計算卡爾曼增益
K = P_*H'/(H*P_*H'+R);
% 得到當前狀態的最優化估算值 增益乘以殘差
X = X_+K*(Z(i)-H*X_);
%更新K狀態的協方差
P = (eye(2)-K*H)*P_;
scatter(X(1), X(2),4); %畫點,橫軸表示位置,縱軸表示速度
end
end
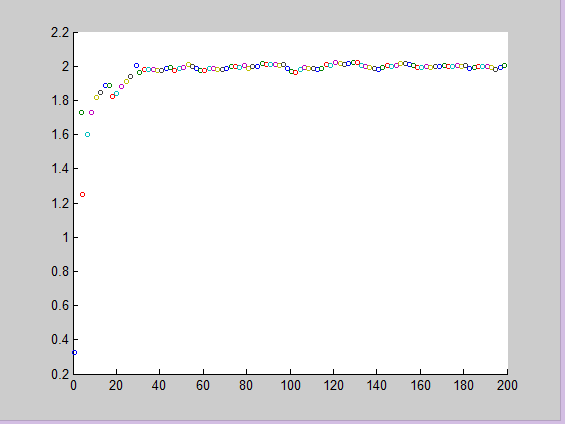
其中 x 軸為位置,y軸為速度。
在代碼中,我們設定x的變化是 1:2:200,則速度就是2,可以由上圖看到,值經過幾次迭代,速度就基本上在 2 附近擺動,擺動的緣由是我們加入了噪聲。
接下來來看1個實際例子。
我們的數據為 data = [149.360 , 150.06, 151.44, 152.81,154.19 ,157.72];
這是應用光流法從視頻中獲得角點的實際x軸坐標,總共有6個數據,也就是代表了1個點的連續6幀的x軸坐標。接下來這個例子,我們將實現用5幀的數據進行訓練,然后預測出第6幀的x軸坐標。
在上1個matlab例子中,我們的訓練數據比較多,因此我們的初始狀態設置為[0,0],也就是位置為0,速度為0,在訓練數據比較多的情況下,初始化數據為0并沒有關系,由于我們在上面的效果圖中可以看到,算法的經太短暫的迭代就可以夠發揮作用。
但在這里,我們的訓練數據只有5幀,所以為了加快訓練,我們將位置狀態初始化為第1幀的位置,速度初始化為第2幀與第1幀之差。
KF.m
function [predData,dataX] = KF(dataZ)
%%
%
% Description : kalmanFiltering
% Author : Liulongpo
% Time:2015⑷⑵9 16:42:34
%
%%
Z = dataZ';
len = length(Z);
%Z=(1:2:200); %觀測值 汽車的位置 也就是我們要修改的量
noise=randn(1,len); %方差為1的高斯噪聲
dataX = zeros(2,len);
Z=Z+noise;
X=[Z(1) ; Z(2)-Z(1) ]; %初始狀態 分別為 位置 和速度
P=[1 0;0 1]; %狀態協方差矩陣
F=[1 1;0 1]; %狀態轉移矩陣
Q=[0.0001,0;0 , 0.0001]; %狀態轉移協方差矩陣
H=[1,0]; %觀測矩陣
R=1; %觀測噪聲方差
%figure;
%hold on;
for i = 1:len
%基于上1狀態預測當前狀態
% 2x1 2x1
X_ = F*X;
% 更新協方差 Q系統進程的協方差 這兩個公式是對系統的預測
% 2x1 2x1 1x2 2x2
P_ = F*P*F'+Q;
% 計算卡爾曼增益
K = P_*H'/(H*P_*H'+R);
% 得到當前狀態的最優化估算值 增益乘以殘差
X = X_+K*(Z(i)-H*X_);
%更新K狀態的協方差
P = (eye(2)-K*H)*P_;
dataX(:,i) = [X(1);X(2)];
%scatter(X(1), X(2),4); %畫點,橫軸表示位置,縱軸表示速度
end
predData = F*X;
endtestKF.m
function testKF
%%
clc
close all
%%
%data = load('D:a.txt');
%data = [149.360 , 150.06, 151.44, 152.81,154.19,157.72,157.47,159.33,153.66];
data = [149.360 , 150.06, 151.44, 152.81,154.19 ,157.72];
[predData , DataX] = KF(data');
error = DataX(1,:) - data;
i = 1:length(data);
figure
subplot 311
scatter(i,data,3),title('原始數據')
subplot 312
scatter(i,DataX(1,:),3),title('預測數據')
subplot 313
scatter(i,error,3),title('預測誤差')
predData(1)
%{
scatter(i,error,3);
figure
scatter(i,data,3)
figure
scatter(i,predData(1,:),3)
%}
end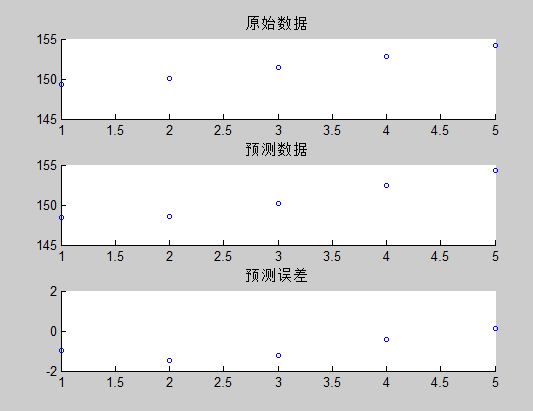
預測結果為: 155.7493 ,跟實際結果 157.72 唯一1.9 的誤差,可以看到,卡爾曼濾波器算法對少許數據的預測效果還是挺不錯的。固然,預測位置的同時,我們也得到了預測速度。
參考文獻: 視頻: 卡爾曼濾波的原理和在MATLAB中的實現
