您當前位置：首頁 > 數據庫 > 數據庫應用 > 數據結構 - 線索二叉樹

數據結構 - 線索二叉樹

來源：程序員人生發布時間：2015-08-14 08:38:14 閱讀次數：6167次

線索樹

  遍歷2叉樹是按1定的規則將樹中的結點排列成1個線性序列，即是對非線性結構的線性化操作。

如何找到遍歷進程中動態得到的每一個結點的直接先驅和直接后繼(第1個和最后1個除外)?如何保存這些信息?

問：1棵有n個結點的2叉樹，有多少個空閑指針域未用？

    若1棵2叉樹有n個結點，則有n⑴條指針連線 ， 而n個結點共有2n個指針域(Lchild和Rchild) ，所以有n+1個空閑指針域未用。
可以利用這些空閑的指針域來寄存結點的直接先驅和直接后繼信息。

對結點的指針域做以下規定：
◆ 若結點有左孩子，則Lchild指向其左孩子，否則，指向其直接先驅；
◆ 若結點有右孩子，則Rchild指向其右孩子，否則，指向其直接后繼；

線索2叉樹的結點結構

用這類結點結構構成的2叉樹存儲結構；叫做線索鏈表；指向結點先驅和后繼的指針叫做線索；依照某種次序遍歷，加上線索的2叉樹稱之為線索2叉樹。

線索2叉樹的結點結構與示例
typedef struct BiTreeNode
{   ElemType  data;
struct BiTreeNode *Lchild , *Rchild ; 
int  Ltag , Rtag ;
}BiThrNode ;

如何在線索樹中找結點的直接后繼?以圖 ，所示的中序線索樹為例：

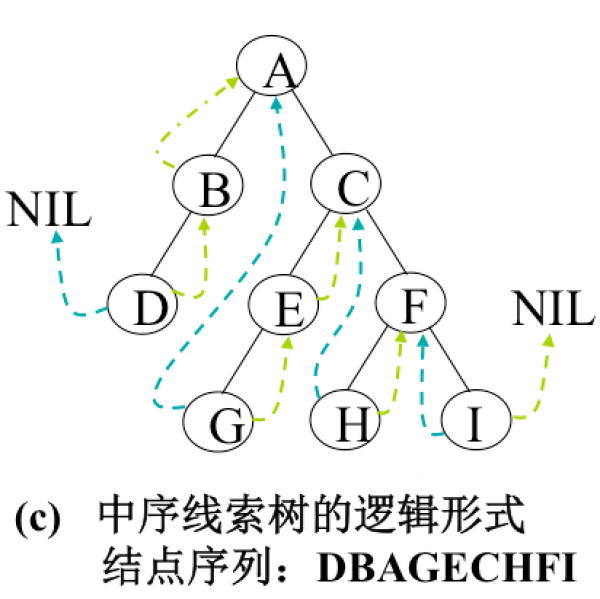
這里寫圖片描述

◆ 若樹中結點的右鏈是線索（Rtag=1），則右鏈直接唆使了結點的直接后繼，如結點G的直接后繼是結點E。
◆ 若樹中結點的右鏈是指針（ Rtag=0）。根據中序遍歷的規律， Rtag=0的結點的直接后繼是遍歷其右子樹時訪問的第1個結點，即右子樹中最左下位置的(葉子)結點。如結點C的直接后繼：沿右指針找到右子樹的根結點F，然后沿左鏈往下直到Ltag=1的結點即為C的直接后繼結點H。

后序遍歷線索樹

在后序遍歷的線索樹中找結點的直接后繼比較復雜，可分以下3種情況：

若結點是2叉樹的根結點：其直接后繼為空；
若結點是其父結點的左孩子且其父結點沒有右子樹：直接后繼為其父結點；
若結點是其父結點的左孩子且其父結點有右子樹：直接后繼是對其父結點的右子樹按后序遍歷的第1個結點。

線索化2叉樹

2叉樹的線索化指的是依照某種遍歷次序使2叉樹成為線索2叉樹的進程。

線索化的進程就是在遍歷進程中修改空指針使其指向直接先驅或直接后繼的進程。
   下面主要討論按中序遍歷次序線索化2叉樹。
   仿照線性表的存儲結構，在2叉樹的線索鏈表上也添加1個頭結點head，頭結點的指針域的安排是：

◆ Lchild域：指向2叉樹的根結點；
◆ Rchild域：指向中序遍用時的最后1個結點；
◆ 2叉樹中序序列中的第1個結點Lchild指針域和最后1個結點Rchild指針域均指向頭結點head。

  添加了頭結點的線索2叉樹，猶如為2叉樹建立了1個雙向線索鏈表，對1棵線索2叉樹既可從頭結點也可從最后1個結點開始按尋覓直接后繼進行遍歷。明顯，這類遍歷不需要堆棧。

#define  MAX_NODE   50
typedef enmu{ Link , Thread} PointerTag ;
/*  Link=0表示指針， Thread=1表示線索   */
typedef struct BiThrNode
{   ElemType  data;
struct BiTreeNode *Lchild , *Rchild ; 
PointerTag  Ltag , Rtag ;
}BiThrNode, *BiThrTree;

按先序序列構造2叉線索樹

ElemType Nil=‘#’;   /*以#為空 */
Status CreateBiThrTree(BiThrTree *T)
{      ElemType ch;
       scanf("%c",&ch);
    if(h==Nil)  *T=NULL;
    else
    {   *T=(BiThrTree)malloc(sizeof(BiThrNode));
        if(!*T) return ERROR;
        (*T)->data=ch; /* 生成根結點(前序) */
        CreateBiThrTree(&(*T)->lchild); /* 遞歸構造左子樹 */
        if((*T)->lchild)    (*T)->LTag=Link; /* 有左孩子 */
        CreateBiThrTree(&(*T)->rchild); /* 遞歸構造右子樹 */
        if((*T)->rchild)   (*T)->RTag=Link; /* 有右孩子 */
    }
    return OK;
}

中序遍歷線索化的遞歸函數

BiThrNode *pre//全局變量，始終指向剛剛訪問過的結點
void  InThreading (BiThrNode *T)
{   if(T)
    {  Inorder_Threading(T->lchild) /* 遞歸左子樹線索化 */
    if(!T->lchild) /* 沒有左孩子 */
    {      T->LTag=Thread; /* 先驅線索 */
        T->lchild=pre; /* 左孩子指針指向先驅 */
     }
    if(!pre->rchild) /* 先驅沒有右孩子 */
    {       pre->RTag=Thread; /* 后繼線索 */
         pre->rchild=T; /* 先驅右孩子指針指向后繼(當前結點T) */
      }
      pre=T; /* 保持pre指向T的先驅 */
      Inorder_Threading(T->rchild); /* 遞歸右子樹線索化 */
    }
}

先驅結點的線索化：if(!T->lchild)表示如果某結點的左指針域為空，由于其先驅結點剛剛訪問過，賦值給了pre，所以可將pre賦值給T->lchild，并修改T->LTag=Thread（即定義為1）以完成先驅結點的線索化；

后繼結點的線索化：因此時后繼結點還沒有訪問到，因此只能對它的先驅結點pre的右指針rchild做判斷， if(!pre->rchild)表示如果先驅的右指針域為空，則T就是pre的后繼，因而pre->rchild=T，并且設置pre->RTag=Thread，完成后繼結點的線索化。

完成先驅和后繼的判斷后，要將當前結點T賦值給pre，以便于下次使用。

/* 中序遍歷2叉樹T,并將其中序線索化,Thrt指向頭結點 */
Status InOrderThreading(BiThrTree *Thrdhead, BiThrTree T)
{   * Thrdhead =(BiThrTree)malloc(sizeof(BiThrNode));
     if(!* Thrdhead )  return ERROR;
    (* Thrdhead )->LTag=Link; /* 建頭結點 */
    (* Thrdhead )->RTag=Thread;
    (* Thrdhead )->rchild= NULL; //右指針此時為空
    if(!T)   (* Thrdhead )->lchild= * Thrdhead; //若2叉樹空,則左指針回指
    else
    {
        (* Thrdhead )->lchild=T; //非空，指向根節點
        pre=(* Thrdhead );
        InThreading(T); /* 中序遍歷進行中序線索化 */
        pre->rchild=* Thrdhead; //pre是中序遍歷的最后1個結點
        pre->RTag=Thread; /* 最后1個結點線索化 */
        (* Thrdhead )->rchild=pre;
    }
    return OK;
}

線索2叉樹遍歷

    線索2叉樹的創建雖然比較復雜，但在線索2叉樹中，由于有線索存在，在某些情況下可以方便地找到指定結點在某種遍歷序列中的直接先驅或直接后繼。

   另外，在線索2叉樹上進行某種遍歷比在1般的2叉樹上進行這類遍歷要容易很多，不需要設置堆棧，且算法10分簡潔。

/* 中序遍歷2叉線索樹T(頭結點)的非遞歸算法 */
Status InOrderTraverse_Thr(BiThrTree T)
{ 
    BiThrTree p;
    p=T->lchild;   /* p指向根結點 */
    while(p!=T)  /* 空樹或遍歷結束時,p==T */
    {      while(p->LTag==Link)
            p=p->lchild; //當LTag==0時循環到中序序列第1個結點
        visit(p->data);
        while(p->RTag==Thread&&p->rchild!=T)
        {
            p=p->rchild;
            visit(p->data); /* 訪問后繼結點 */
        }
        p=p->rchild;
    }
    return OK;
}