耗時(shí)3節(jié)課 充分體現(xiàn)出粗心釀成大錯(cuò)這個(gè)道理 1開始1直不知道為何數(shù)組越界 原來是minn和ninj寫反了 后來又由于讀入函數(shù)出問題 反復(fù)調(diào)試 今后1定要注意
題目還是放上吧:
年輕的探險(xiǎn)家來到了1個(gè)印第安部落里。在那里他和酋長的女兒相愛了,因而便向酋長去求親。酋長要他用10000個(gè)金幣作為聘礼才答應(yīng)把女兒嫁給他。探險(xiǎn)家拿不出這么多金幣,便要求酋長下降要求。酋長說:“嗯,如果你能夠替我弄到大祭司的皮襖,我可以只要8000金幣。如果你能夠弄來他的水晶球,那末只要5000金幣就好了。”探險(xiǎn)家就跑到大祭司那里,向他要求皮襖或水晶球,大祭司要他用金幣來換,或替他弄來其他的東西,他可以下降價(jià)格。探險(xiǎn)家因而又跑到其他地方,其他人也提出了類似的要求,或直接用金幣換,或找到其他東西就能夠下降價(jià)格。不過探險(xiǎn)家沒必要用多樣?xùn)|西去換1樣?xùn)|西,由于不會(huì)得到更低的價(jià)格。探險(xiǎn)家現(xiàn)在很需要你的幫忙,讓他用最少的金幣娶到自己的心上人。另外他要告知你的是,在這個(gè)部落里,等級(jí)觀念10分森嚴(yán)。地位差距超過1定限制的兩個(gè)人之間不會(huì)進(jìn)行任何情勢(shì)的直接接觸,包括交易。他是1個(gè)外來人,所以可以不受這些限制。但是如果他和某個(gè)地位較低的人進(jìn)行了交易,地位較高的的人不會(huì)再和他交易,他們認(rèn)為這樣等因而間接接觸,反過來也1樣。因此你需要在斟酌所有的情況以后給他提供1個(gè)最好的方案。
為了方便起見,我們把所有的物品從1開始進(jìn)行編號(hào),酋長的承諾也看做1個(gè)物品,并且編號(hào)總是1。每一個(gè)物品都有對(duì)應(yīng)的價(jià)格P,主人的地位等級(jí)L,和1系列的替換品Ti和該替換品所對(duì)應(yīng)的“優(yōu)惠”Vi。如果兩人地位等級(jí)差距超過了M,就不能“間接交易”。你必須根據(jù)這些數(shù)據(jù)來計(jì)算出探險(xiǎn)家最少需要多少金幣才能娶到酋長的女兒。
輸入包括了多個(gè)測試數(shù)據(jù)。每一個(gè)測試數(shù)據(jù)的第1行是兩個(gè)整數(shù)M,N(1<=N<=100),順次表示地位等級(jí)差距限制和物品的總數(shù)。接下來依照編號(hào)從小到大順次給出了N個(gè)物品的描寫。每一個(gè)物品的描寫開頭是3個(gè)非負(fù)整數(shù)P、L、X(X<N),順次表示該物品的價(jià)格、主人的地位等級(jí)和替換品總數(shù)。接下來X行每行包括兩個(gè)整數(shù)T和V,分別表示替換品的編號(hào)和“優(yōu)惠價(jià)格”。
對(duì)每一個(gè)測試數(shù)據(jù),在單唯一行內(nèi)輸出最少需要的金幣數(shù)。
1 4
10000 3 2 //酋長的承諾
2 8000
3 5000
1000 2 1 //大祭司的皮襖
4 200
3000 2 1 //大祭司的水晶球
4 200
50 2 0 // 其他某件物品
5250
方便大家理解,畫了1張很低劣的圖,大家湊活看1下
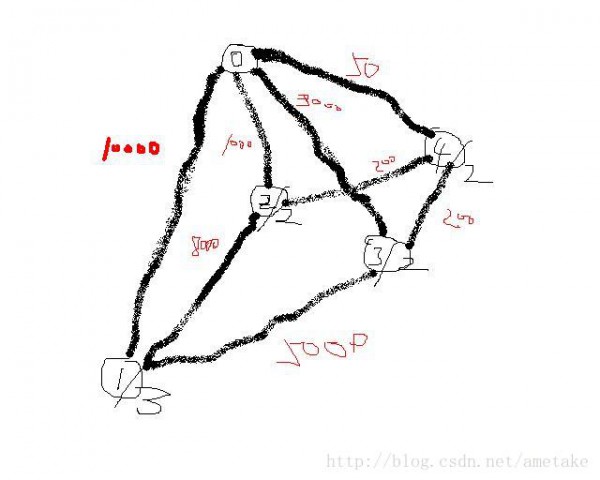
代碼放上:
在這里還要特別說明1下大整數(shù)常量的定義
const
int
maxn=0x3f3f3f3f;
這真是極好的存在= =援用1下1篇已消失的博文的解釋(順便吐槽域名重定向去了甚么鬼地方):
0x3f3f3f3f的10進(jìn)制是1061109567,也就是10^9級(jí)別的(和0x7fffffff1個(gè)數(shù)量級(jí)),而1般場合下的數(shù)據(jù)都是小于10^9的,所以它可以作為無窮大使用而不致出現(xiàn)數(shù)據(jù)大于無窮大的情形。
另外一方面,由于1般的數(shù)據(jù)都不會(huì)大于10^9,所以當(dāng)我們把無窮大加上1個(gè)數(shù)據(jù)時(shí),它其實(shí)不會(huì)溢出(這就滿足了“無窮大加1個(gè)有窮的數(shù)仍然是無窮大”),事實(shí)上0x3f3f3f3f+0x3f3f3f3f=2122219134,這非常大但卻沒有超過32-bit int的表示范圍,所以0x3f3f3f3f還滿足了我們“無窮大加無窮大還是無窮大”的需求。
最后,0x3f3f3f3f還能給我們帶來1個(gè)意想不到的額外好處:如果我們想要將某個(gè)數(shù)組清零,我們通常會(huì)使用memset(a,0,sizeof(a))這樣的代碼來實(shí)現(xiàn)(方便而高效),但是當(dāng)我們想將某個(gè)數(shù)組全部賦值為無窮大時(shí)(例如解決圖論問題時(shí)鄰接矩陣的初始化),就不能使用memset函數(shù)而得自己寫循環(huán)了(寫這些不重要的代碼真的很痛苦),我們知道這是由于memset是按字節(jié)操作的,它能夠?qū)?shù)組清零是由于0的每一個(gè)字節(jié)都是0,現(xiàn)在好了,如果我們將無窮大設(shè)為0x3f3f3f3f,那末奇跡就產(chǎn)生了,0x3f3f3f3f的每一個(gè)字節(jié)都是0x3f!所以要把1段內(nèi)存全部置為無窮大,我們只需要memset(a,0x3f,sizeof(a))。
所以在通常的場合下,0x3f3f3f3f真的是1個(gè)非常棒的選擇。
總結(jié)起來就是3句話
1 夠大,1般這么大你不會(huì)用到
2 夠大但不容易溢出
3 方便數(shù)組賦值(如果你用FF會(huì)變成負(fù)數(shù),符號(hào)位也會(huì)成1)
1輪開始了,該來的總會(huì)來的。
歡迎小花加入C黨大家族,本科同學(xué)你現(xiàn)在是1個(gè)人了,摸頭???祝小花的喜家家之路1帆風(fēng)順。
――君子博學(xué)而日參省乎己,則知明而行無過矣。
