520E - Pluses everywhere/521C - Pluses everywhere
Idea: Endagorion
Preparation: gchebanov, DPR-pavlin
Consider some way of placing all the pluses, and a single digit di (digits in the string are numbered starting from 0 from left to right). This digit gives input of di?10l to the total sum, where l is the distance to the nearest plus from the right, or to the end of string if there are no pluses there. If we sum up these quantities for all digits and all ways of placing the pluses, we will obtain the answer.
For a given digit di and some fixed l, how many ways are there to place the pluses? First of all, consider the case when the part containing the digit di is not last, that is, i?+?l?<?n?-?1. There are n?-?1 gaps to place pluses in total; the constraint about di and the distance l means that after digits di, ..., di?+?l?-?1 there are no pluses, while after the digit di?+?l there should be a plus. That is, the string should look as follows:
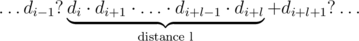
Here a dot means a gap without a plus, and a question mark means that it's not important whether there is a plus or not. So, out of n?-?1possible gaps
there are l?+?1 gaps which states are defined, and there is one plus used in these gaps. That means that the other (n?-?1)?-?(l?+?1)?=?n?-?l?-?2 gaps
may contain k?-?1 pluses in any possible way; that is, the number of such placements is 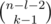 .
A similar reasoning implies that if the digit di is
in the last part, that is, i?+?l?=?n?-?1, the number of placements is
.
A similar reasoning implies that if the digit di is
in the last part, that is, i?+?l?=?n?-?1, the number of placements is 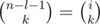 .
.
To sum up, the total answer is equal to
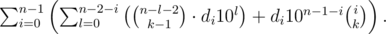
Let us transform the sum:
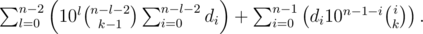
To compute these sums, we will need to know all powers of 10 up to n-th (modulo 109?+?7),
along with the binomial coefficients. To compute the binomials, recall that 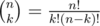 ,
so it is enough to know all the numbers k! for k upto n,
along with their modular inverses. Also we should use the prefix sums of di,
that is, the array
,
so it is enough to know all the numbers k! for k upto n,
along with their modular inverses. Also we should use the prefix sums of di,
that is, the array 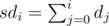 .
The rest is simple evaluation of the above sums.
.
The rest is simple evaluation of the above sums.
The total complexity is 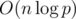 ,
because the common algorithms for modular inverses (that is, Ferma's little theorem exponentiation or solving a diophantine equation using the Euclid's algorithm) have theoritcal worst-case complexity of
,
because the common algorithms for modular inverses (that is, Ferma's little theorem exponentiation or solving a diophantine equation using the Euclid's algorithm) have theoritcal worst-case complexity of 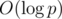 .
However, one can utilize a neat trick for finding modular inverses for first n consecutive numbers in linear time for a total complexity of O(n);
for the description of the method refer to this comment by Kaban⑸ (not
sure why it has a negative rating, I found this quite insightful; maybe anyone can give a proper source for this method?).
.
However, one can utilize a neat trick for finding modular inverses for first n consecutive numbers in linear time for a total complexity of O(n);
for the description of the method refer to this comment by Kaban⑸ (not
sure why it has a negative rating, I found this quite insightful; maybe anyone can give a proper source for this method?).
Challenge: now we want to find the sum of all expressions that are made by placing k pluses with a?≤?k?≤?b; that is, we want to find the sum of the answers for the original problem with k?=?a,?...,?b; here a and b can be any integers with 0?≤?a?≤?b?≤?n?-?1. There is an obviousO(n2) solution: just find the answers for all k separately. Can you find a linear solution?
Vasya is sitting on an extremely boring math class. To have fun, he took a piece of paper and wrote out n numbers on a single line. After that, Vasya began to write out different ways to put pluses ("+") in the line between certain digits in the line so that the result was a correct arithmetic expression; formally, no two pluses in such a partition can stand together (between any two adjacent pluses there must be at least one digit), and no plus can stand at the beginning or the end of a line. For example, in the string 100500, ways 100500 (add no pluses), 1+00+500 or 10050+0 are correct, and ways 100++500, +1+0+0+5+0+0 or 100500+ are incorrect.
The lesson was long, and Vasya has written all the correct ways to place exactly k pluses in a string of digits. At this point, he got caught having fun by a teacher and he was given the task to calculate the sum of all the resulting arithmetic expressions by the end of the lesson (when calculating the value of an expression the leading zeros should be ignored). As the answer can be large, Vasya is allowed to get only its remainder modulo 109?+?7. Help him!
The first line contains two integers, n and k (0?≤?k?<?n?≤?105).
The second line contains a string consisting of n digits.
Print the answer to the problem modulo 109?+?7.
In the first sample the result equals (1?+?08)?+?(10?+?8)?=?27.
In the second sample the result equals 1?+?0?+?8?=?9.
