寫在前面
前面為本節內容準備了向量和矩陣、線性變換等內容，本節開始學習OpenGL中的坐標處理。OpenGL中的坐標處理進程包括模型變換、視變換、投影變換、視口變換等內容，這個主題的內容有些多，因此分節學習，主題將分為5節內容來學習。本節主要學習模型變換。本節示例代碼都可在我的github處下載。
通過本節可以了解到
OpenGL中的坐標處理包括模型變換、視變換、投影變換、視口變換等內容，具體進程以下圖1所示:
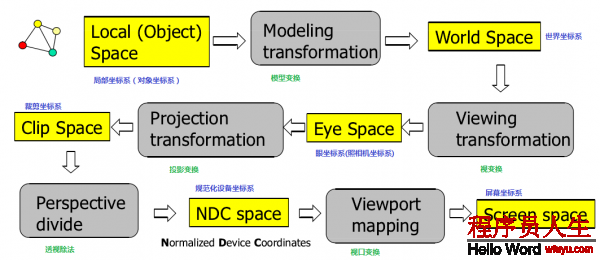
每個進程處理都有其緣由，這些內容計劃將會在不同節里分別介紹，最后再整體掌控1遍。
今天我們學習第1個階段——模型變換。
我們在OpenGL中通過定義1組頂點來定義1個模型，或通過其他3D建模軟件事前建好模型然后導入到OpenGL中。頂點屬性定義了模型。如果我們要在1個場景中不同位置顯示同1個模型怎樣辦？ 如果我們要以不同的比例、不同角度顯示同1個模型又怎樣辦 ？
如果繼續以類似的頂點屬性數據定義同1個模型，調劑它滿足上述需求的話，不但浪費顯卡內存，而且這個調劑的工作量也很大，因此效力很低。更好地解決方法是，我們定義的模型根據需要可以履行放大、縮小等操作來不同比例顯示，可以通過平移來放在不同位置，可以通過旋轉來按不同角度顯示。這類方式就是履行模型變換。
模型變換通過對模型履行平移(translation)、縮放(scale)、旋轉(rotation)、鏡像(reflection)、錯切(shear)等操作，來調劑模型的進程。通過模型變換，我們可以依照公道方式指定場景中物體的位置等信息。
平移就是將物體從1個位置
如果對向量和矩陣不熟習，可以回過去看前面介紹的向量和矩陣；如果對上面使用的齊次坐標系不熟習，可以回過去看前面介紹的線性變換部份。
本節的模型變換在OpenGL程序中，可使用GLM數學庫實現。例如平移變換實現以下：
glm::mat4 model; // 構造單位矩陣
model = glm::translate(model, glm::vec3(-0.5f, 0.0f, 0.0f));上述表示平移向量為(-0.5,0.0,0.0)，得到1個平移矩陣存儲到model中。
在程序中我們繪制了4個矩形，通過平移將其放在不同位置，效果以下圖所示：
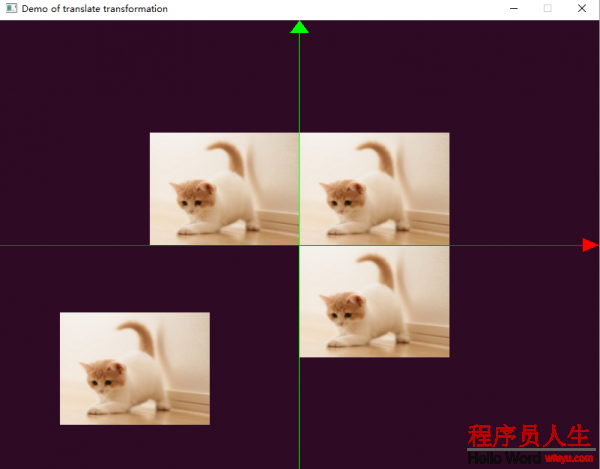
在上圖示例中，我們使用不同的著色器還繪制了坐標軸，坐標軸通過箭頭和軸線繪制。在xoy坐標系中，第1個象限為原圖，第2個象限為平移(-0.5,0.0,0.0)后的矩形,第3象限為平移(-0.8,-0.8,0.0)后的矩形，第4個象限為平移(0.0,-0.5,0.0)后的矩形。
注意 通過上面坐標處理的全局進程圖1可以看到，實際頂點輸出還需要經過視變換、投影變換進程等處理，本節主要討論模型變換，因此我們在代碼中，不斟酌視變換和投影變換，使用默許的視變換和投影變換，即這兩個變換保持為單位矩陣。默許的方式就是我們1直在使用的正交投影方式。變換矩陣在著色器中使用uniform變量傳遞，在c++程序中使用glm::mat4與之對應。對uniform變量不熟習的話，可以回過頭去看2D紋理部份的使用方法。
設置默許視變換和投影變換矩陣的代碼以下：
glm::mat4 projection;// 投影變換矩陣
glm::mat4 view; // 視變換矩陣
glm::mat4 model; // 模型變換矩陣
glUniformMatrix4fv(
glGetUniformLocation(shader.programId,"projection"),
1, GL_FALSE, glm::value_ptr(projection));
glUniformMatrix4fv(
glGetUniformLocation(shader.programId,"view"),
1,GL_FALSE, glm::value_ptr(view));繪制4個矩形的代碼為：
// 繪制第1個矩形
glUniformMatrix4fv(
glGetUniformLocation(shader.programId, "model"),
1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);
// 繪制第2個矩形
model = glm::mat4();
model = glm::translate(model, glm::vec3(-0.5f, 0.0f, 0.0f));
glUniformMatrix4fv(
glGetUniformLocation(shader.programId, "model"),
1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);
// 繪制第3個矩形
model = glm::mat4();
model = glm::translate(model, glm::vec3(-0.8f, -0.8f, 0.0f));
glUniformMatrix4fv(
glGetUniformLocation(shader.programId, "model"), 1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);
// 繪制第4個矩形
model = glm::mat4();
model = glm::translate(model, glm::vec3(0.0f, -0.5f, 0.0f));
glUniformMatrix4fv(
glGetUniformLocation(shader.programId, "model"),1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);這里繪制矩形使用的頂點屬性數據，和紋理使用方法，可以回過頭去查看上1節2D紋理映照內容。
本節繪制矩形的頂點著色器中都使用代碼：
#version 330
layout(location = 0) in vec3 position;
layout(location = 1) in vec3 color;
layout(location = 2) in vec2 textCoord;
out vec3 VertColor;
out vec2 TextCoord;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
void main()
{
gl_Position =
projection * view * model * vec4(position, 1.0);
VertColor = color;
TextCoord = textCoord;
}本節繪制矩形的片元著色器中都使用代碼：
#version 330
in vec3 VertColor;
in vec2 TextCoord;
uniform sampler2D tex;
out vec4 color;
void main()
{
color = texture(tex, vec2(TextCoord.s, 1.0 -TextCoord.t) );
}代碼中使用坐標vec2(TextCoord.s, 1.0 -TextCoord.t)表示將紋理的y軸翻轉，避免紋理倒立顯示。
在座標和變換的數學基礎1節中，我們已提到，對4x4仿射變換矩陣，可以表示平移(仿射變換)、縮放、旋轉等線性變換，其中矩陣的情勢為：
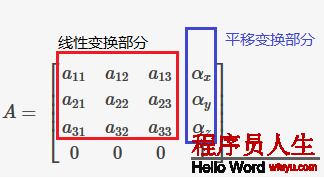
記住這1點，對矩陣情勢理解會比較清楚。
縮放可以沿著3個坐標軸的方向獨立進行，當縮放參數1致時是均勻縮放，否則是非均勻縮放。對以原點為中心的縮放來說，根據坐標和變換的數學基礎，1節所得到的結論：線性變換矩陣為變換后基向量組成。縮放因子為
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈
上一篇 Redis
程序員人生，我編程，我富裕，記住wfuyu網，php教程，php學習，php手冊，CMS模版制作
聲明：本站大部分內容是作者原創，少部分收集于互聯網供大家一起學習，原版權很多不明，如有侵權請聯系本站，謝謝！
粵ICP備14040726號-1?? 2015-2020 程序員人生 版權所有
