017-Prim算法-貪心-《算法設計技巧與分析》M.H.A學習筆記
來源:程序員人生 發布時間:2016-06-30 08:42:24 閱讀次數:2766次
基本思路:
定義結點集合U, V (U表示已選擇加入MST的結點集合,V表示未選)
1. 任選1個結點加入U
2. 選擇1條邊權最小的邊,他的兩個結點分別屬于U, V,并把屬于V的那個結點加入U
3. 重復履行2直到V空
偽代碼:
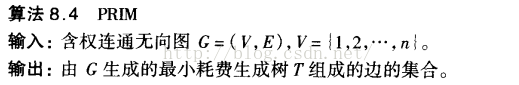

C++代碼:
int g[mnx][mnx];
int n, m;
int d[mnx];
// 樸素 prim, 復雜度O(|V|^2) |V|:點數, |E|:邊數
int prim() {
memset(d, 0x3f, sizeof d); //初始化
int ret = d[1] = 0; // 先把d[1]弄成0
for(int i = 1; i <= n; ++i) {
int u = ⑴;
for(int j = 1; j <= n; ++j) //找到d[u]最小的1個u
if((u == ⑴ || d[u] > d[j]) && d[j] != ⑴)
u = j;
ret += d[u];
d[u] = ⑴;
for(int j = 1; j <= n; ++j) // 更新和u鄰接的節點的d[j]值
d[j] = min(d[j], g[u][j]);
}
return ret;
}
算法分析:
主要耗費在查找邊權最小的邊,這1步的2重循環耗費Θ(n2),所以算法的時間復雜度為Θ(n2)。
堆優化改進:
我們用小頂堆來完成查找最小邊,和Dijkstra算法1樣,算法共進行了n⑴次插入、n⑴次刪除、m-n+1次Siftup運算。總的時間復雜度為O(mlogn)。
偽代碼:


C++代碼:
int fst[mnx], nxt[mxe], cost[mxe], to[mxe], e;
void init() {
memset(fst, ⑴, sizeof fst);
e = 0;
}
void add(int u, int v, int c) {
to[e] = v, nxt[e] = fst[u], cost[e] = c, fst[u] = e++;
}
struct node {
int u, dis;
node(int u, int dis):u(u), dis(dis) {}
bool operator < (const node &b) const {
return dis > b.dis;
}
};
//堆優化, 復雜度O(|E|log|V|), 稠密圖時比較慢
int primHeap() {
memset(d, 0x3f, sizeof d);
d[1] = 0;
priority_queue<node> q;
q.push(node(1,0)); // 先選定第1個節點
int ret = 0;
while(!q.empty()) {
int u = q.top().u;
int dd = q.top().dis;
q.pop();
if(d[u] != dd) continue; // 如果是被更新之前的值的話就不取, continue掉
ret += dd;
d[u] = ⑴;
for(int j = fst[u]; ~j; j = nxt[j]) {
int v = to[j], c = cost[j]; // 更新
if(d[v] > c && d[v] != ⑴) {
d[v] = c;
q.push(node(v, c));
}
}
}
return ret;
}
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈