您當(dāng)前位置：首頁 > php開源 > php教程 > 算法#14--詳解各種字符串查找算法和代碼實(shí)現(xiàn)

算法#14--詳解各種字符串查找算法和代碼實(shí)現(xiàn)

來源：程序員人生發(fā)布時(shí)間：2016-10-06 09:13:49 閱讀次數(shù)：2918次

1.算法匯總

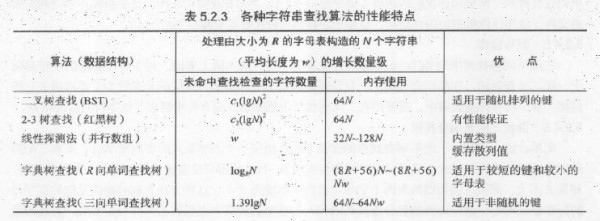
首先，來看1張各種字符串查找算法的匯總。前面的文章已介紹過2叉樹查找和紅黑樹查找。這里不在介紹。

本文重點(diǎn)介紹后面3種查找算法：線性探測法、R向單詞查找樹和3向單詞查找樹。

2.線性探測法

實(shí)現(xiàn)散列表的另外一種方式是用大小為M的數(shù)組保存N個(gè)鍵值對(duì)，其中M>N。依托數(shù)據(jù)中的空位解決碰撞沖突。基于這類策略的所有方法都統(tǒng)稱為開放地址散列表。其中最簡單的方法叫做線性探測法：當(dāng)碰撞產(chǎn)生時(shí)，直接檢查散列表的下1個(gè)位置（索引加1），可能產(chǎn)生3種結(jié)果：

命中，該位置的鍵和被查找的鍵相同；
未命中，鍵為空（該位置沒有鍵）；
繼續(xù)查找，該位置的鍵和被查找的鍵不同。

其核心思想是與其將內(nèi)存用作鏈表，不如將它們作為散列表的空元素。即用散列函數(shù)找到索引，檢查其中的鍵和被查找的鍵是不是相同。如果不同則繼續(xù)查找（增加索引，到達(dá)數(shù)組結(jié)尾后再折回?cái)?shù)組開頭），直到找到該鍵或遇到1個(gè)空元素。進(jìn)程以下圖所示：

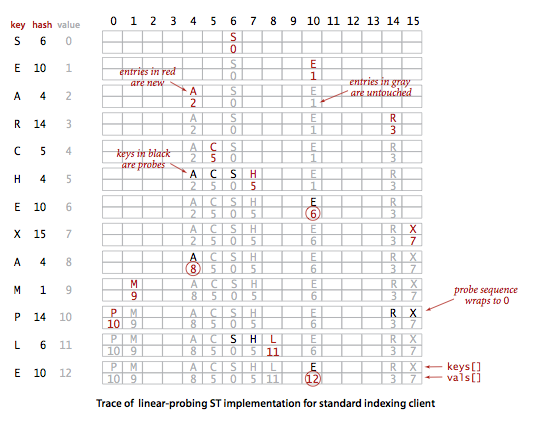
在基于線性探測法的散列表中履行刪除操作比較復(fù)雜，如果將該鍵所在位置為為null是不行的。需要將簇中被刪除鍵的右邊的所有鍵重新插入散列表。

代碼實(shí)現(xiàn)：


//基于線性探測的符號(hào)表
public class LinearProbingHashST<Key,Value> 
{
    private static final int INIT_CAPACITY = 16;

    private int n;// 鍵值對(duì)數(shù)量
    private int m;// 散列表的大小
    private Key[] keys;// 保存鍵的數(shù)組
    private Value[] vals;// 保存值的數(shù)組

    public LinearProbingHashST() 
    {
        this(INIT_CAPACITY);
    }

    @SuppressWarnings("unchecked")
    public LinearProbingHashST(int capacity) 
    {
        this.m = capacity;
        keys = (Key[]) new Object[capacity];
        vals = (Value[]) new Object[capacity];
    }

    public int hash(Key key)
    {
        return (key.hashCode() & 0x7fffffff) % m;
    }

    public void put(Key key, Value val)
    {
        if(key == null) 
        {
            throw new NullPointerException("key is null");
        }

        if(val == null)
        {
            delete(key);
            return;
        }

        // TODO擴(kuò)容
        if(n >= m/2)
        {
            resize(2*m);
        }

        int i = hash(key);
        for (; keys[i] != null; i = (i + 1) % m) 
        {
            if(key.equals(keys[i]))
            {
                vals[i] = val;
                return;
            }
        }

        keys[i] = key;
        vals[i] = val;
        n++;
    }

    public void delete(Key key)
    {
        if(key == null) 
        {
            throw new NullPointerException("key is null");
        }

        if (!contains(key)) 
        {
            return;
        }

        // 找到刪除的位置
        int i = hash(key);
        while (!key.equals(keys[i])) 
        {
            i = (i + 1) % m;
        }

        keys[i] = null;
        vals[i] = null;

        // 將刪除位置后面的值重新散列
        i = (i + 1) % m;
        for (; keys[i] != null; i = (i + 1) % m) 
        {
            Key keyToRehash = keys[i];
            Value valToRehash = vals[i];
            keys[i] = null;
            vals[i] = null;
            n--;
            put(keyToRehash, valToRehash);
        }

        n--;
        // TODO縮容
        if(n>0 && n == m/8)
        {
            resize(m/2);
        }
    }

    public Value get(Key key)
    {
        if(key == null) 
        {
            throw new NullPointerException("key is null");
        }

        for (int i = hash(key); keys[i] != null; i = (i + 1) % m) 
        {
            if(key.equals(keys[i]))
            {
                return vals[i];
            }
        }
        return null;
    }

    public boolean contains(Key key)
    {
        if(key == null) 
        {
            throw new NullPointerException("key is null");
        }

        return get(key) != null;
    }   

    private void resize(int cap)
    {
        LinearProbingHashST<Key,Value> t;
        t = new LinearProbingHashST<Key,Value>(cap);
        for(int i = 0; i < m; i++)
        {
            if(keys[i] != null)
            {
                t.put(keys[i], vals[i]);
            }
        }
        keys = t.keys;
        vals = t.vals;
        m = t.m;
    }

     public static void main(String[] args) 
     { 
         LinearProbingHashST<String, String> st = new LinearProbingHashST<String, String>();
         String[] data = new String[]{"a", "b", "c", "d", "e", "f", "g", "h", "m"};
         String[] val = new String[]{"aaa", "bbb", "ccc", "ddd", "eee", "fff", "ggg", "hhh", "mmm"};
         for (int i = 0; i < data.length; i++)
         {            
            st.put(data[i], val[i]);
         } 

         for (int i = 0; i < data.length; i++)
         {
             System.out.println(data[i] + " " + st.get(data[i]));
         }     
     }
}

3.R向單詞查找樹

3.1 定義

與各種查找樹1樣，單詞查找樹也是由鏈接的結(jié)點(diǎn)所組成的數(shù)據(jù)結(jié)構(gòu)。每一個(gè)結(jié)點(diǎn)只有1個(gè)父結(jié)點(diǎn)（根結(jié)點(diǎn)除外），每一個(gè)結(jié)點(diǎn)都含有R條鏈接，其中R為字母表的大小。每一個(gè)鍵所關(guān)聯(lián)的值保存在該鍵的最后1個(gè)字母所對(duì)應(yīng)的結(jié)點(diǎn)中。值為空的結(jié)點(diǎn)在符號(hào)表中沒有對(duì)應(yīng)的鍵，它們的存在是為了簡化單詞查找樹中的查找操作。

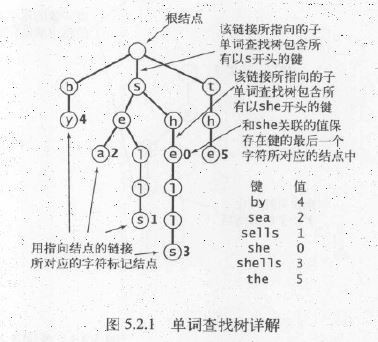
3.2 查找操作

單詞查找樹的查找操作非常簡單，從首字母開始延著樹結(jié)點(diǎn)查找就能夠：

鍵的尾字符所對(duì)應(yīng)的結(jié)點(diǎn)中的值非空，命中！
鍵的尾字符所對(duì)應(yīng)的結(jié)點(diǎn)中的值為空，未命中！
查找結(jié)束于1條空鏈接，未命中！

3.3 插入操作

和2叉查找樹1樣，在插入之前要進(jìn)行1次查找。

在到達(dá)鍵的尾字符之前就遇到了1個(gè)空鏈接。證明不存在匹配的結(jié)點(diǎn)，為鍵中還未被檢查的每一個(gè)字符創(chuàng)建1個(gè)對(duì)應(yīng)的結(jié)點(diǎn)，并將鍵對(duì)應(yīng)的值保存到最后1個(gè)字符的結(jié)點(diǎn)中。
在遇到空鏈接之前就到達(dá)了鍵的尾字符。將該結(jié)點(diǎn)的值設(shè)為鍵對(duì)應(yīng)的值（不管該值是不是為空）。

3.4 刪除操作

刪除的第1步是找到鍵所對(duì)應(yīng)的結(jié)點(diǎn)并將它的值設(shè)為空null. 如果該結(jié)點(diǎn)含有1個(gè)非空的鏈接指向某個(gè)子結(jié)點(diǎn)，那末就不需要再進(jìn)行其他操作了。如果它的所有鏈接均為空，那就需要從數(shù)據(jù)結(jié)構(gòu)中刪除這個(gè)結(jié)點(diǎn)。如果刪除它使得它的父結(jié)點(diǎn)的所有鏈接也均為空，就要繼續(xù)刪除它的父結(jié)點(diǎn)，依此類推。

3.5 代碼實(shí)現(xiàn)


//基于R向單詞查找樹的符號(hào)表
public class TrieST<Value> {
    private static int R = 256; //基數(shù)
    private Node root;
    private static class Node
    {
        private Object val;
        private Node[] next = new Node[R];
    }

    @SuppressWarnings("unchecked")
    public Value get(String key)
    {
        Node x = get(root, key, 0);
        if(x == null)
        {
            return null;
        }
        return (Value)x.val;
    }

    private Node get(Node x, String key, int d)
    {
        //返回以x作為根結(jié)點(diǎn)的字單詞查找樹中與key相干聯(lián)的值
        if(x == null)
        {
            return null;
        }
        if(d == key.length())
        {
            return x;
        }
        char c = key.charAt(d);//找到第d個(gè)字符所對(duì)應(yīng)的字單詞查找樹
        return get(x.next[c], key, d + 1);
    }

    public void put(String key, Value val)
    {
        root = put(root, key, val, 0);          
    }

    private Node put(Node x, String key, Value val, int d)
    {
        //如果key存在于以x為根結(jié)點(diǎn)的子單詞查找樹中則更新與它相干聯(lián)的值
        if(x == null)
        {
            x = new Node();         
        }
        if(d == key.length())
        {
            x.val = val;
            return x;
        }
        char c = key.charAt(d);//找到第d個(gè)字符所對(duì)應(yīng)的字單詞查找樹
        x.next[c] = put(x.next[c], key, val, d + 1);
        return x;
    }

    public void delete(String key)
    {  
        root = delete(root, key, 0); 
    }  

    private Node delete(Node x, String key, int d)
    {  
        if(x == null) 
        {
            return null;  
        }
        if(d == key.length())
        {
            x.val = null;  
        }
        else
        {  
            char c= key.charAt(d);  
            x.next[c] = delete(x.next[c], key, d+1);  
        }  
        if(x.val != null) 
        {
            return x;  
        }

        for(char c = 0; c < R; c++) 
        {
            if(x.next[c] != null) 
            {
                return x; 
            }
        }
        return null;  
    }  

    public static void main(String[] args) 
     {
        TrieST<Integer> newST = new TrieST<Integer>();
        String[] keys= {"Nicholas", "Nate", "Jenny", "Penny", "Cynthina", "Michael"};
        for(int i = 0; i < keys.length; i++)
        {
            newST.put(keys[i], i);
        }           
        newST.delete("Penny");
        for(int i = 0; i < keys.length; i++)
        {
            Object val = newST.get(keys[i]);
            System.out.println(keys[i] + " " + val);
        } 
     }

}

4.3向單詞查找樹

4.1 定義

3向單詞查找樹可以免R向單詞查找樹過度的空間消耗。它的每一個(gè)結(jié)點(diǎn)都含有1個(gè)字符、3條鏈接和1個(gè)值。3條鏈接分別對(duì)應(yīng)當(dāng)前字母小于、等于和大于結(jié)點(diǎn)字母的所有鍵。

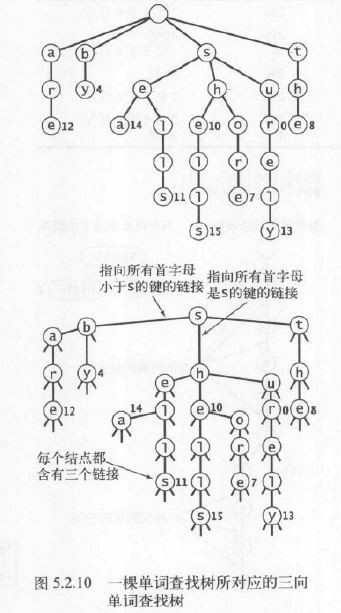
4.1 查找、插入和刪除操作

在查找時(shí)，首先比較鍵的首字母和根結(jié)點(diǎn)的字母。如果鍵的首字母較小，就選擇左鏈接；如果較大，就選擇右鏈接；如果相等則選擇中鏈接。然后遞歸地使用相同的算法。如果遇到1個(gè)空鏈接或當(dāng)鍵結(jié)束時(shí)結(jié)點(diǎn)的值為空，那末查找未命中。如果鍵結(jié)束時(shí)結(jié)點(diǎn)的值非空則查找命中。

插入1個(gè)新鍵時(shí)，首先進(jìn)行查找，然后和單詞查找樹1樣，在樹中補(bǔ)全鍵末尾的所有結(jié)點(diǎn)。

在3向單詞查找樹中，需要使用在2叉查找樹中刪除結(jié)點(diǎn)的方法來刪去與該字符對(duì)應(yīng)的結(jié)點(diǎn)。

4.3 代碼實(shí)現(xiàn)


//基于3向單詞查找樹的符號(hào)表
public class TST<Value> {
    private Node root;
    private class Node
    {
        char c;
        Node left, mid, right;
        Value val;
    }

    public Value get(String key)
    {
        Node x = get(root, key, 0);
        if(x == null)
        {
            return null;
        }
        return x.val;
    }

    private Node get(Node x, String key, int d)
    {
        if(x == null)
        {
            return null;
        }
        char c = key.charAt(d);
        if(c < x.c)
        {
            return get(x.left, key, d);
        }
        else if(c > x.c)
        {
            return get(x.right, key, d);
        }
        else if(d < key.length() - 1)
        {
            return get(x.mid, key, d + 1);
        }
        else
        {
            return x;
        }
    }

    public void put(String key, Value val)
    {
        root = put(root, key, val, 0);
    }

    private Node put(Node x, String key, Value val, int d)
    {
        char c = key.charAt(d);
        if(x == null)
        {
            x = new Node();
            x.c = c;
        }
        if(c < x.c)
        {
            x.left = put(x.left, key, val, d);
        }
        else if(c > x.c)
        {
            x.right = put(x.right, key, val, d);
        }
        else if(d < key.length() - 1)
        {
            x.mid = put(x.mid, key, val, d + 1);
        }
        else
        {
            x.val = val;
        }
        return x;
    }

     public static void main(String[] args) 
     {
            TST<Integer> newTST = new TST<Integer>();
            String[] keys= {"Nicholas", "Nate", "Jenny", "Penny", "Cynthina", "Michael"};
            for(int i = 0; i < keys.length; i++)
            {
                newTST.put(keys[i], i);
            }           

            for(int i = 0; i < keys.length; i++)
            {
                int val = newTST.get(keys[i]);
                System.out.println(keys[i] + " " + val);
            } 
     }
}

它的每一個(gè)結(jié)點(diǎn)只含有3個(gè)鏈接，因此所需空間遠(yuǎn)小于對(duì)應(yīng)的單詞查找樹。使用3向單詞查找樹的最大好處是它能夠很好地適應(yīng)實(shí)際利用中可能出現(xiàn)的被查找鍵的不規(guī)則性。它可使用256個(gè)字符的ASCII編碼或65536個(gè)字符的Unicode編碼，而沒必要擔(dān)心分支帶來的巨大開消。

生活不易，碼農(nóng)辛苦
如果您覺得本網(wǎng)站對(duì)您的學(xué)習(xí)有所幫助,可以手機(jī)掃描二維碼進(jìn)行捐贈(zèng)
程序員人生