Java與算法之(10) - 希爾排序
來源:程序員人生 發布時間:2016-11-03 08:44:24 閱讀次數:2428次
希爾排序是插入排序的1種,是直接插入排序的改進版本。
對上節介紹的直接插入排序法,如果數據原來就已按要求的順序排列,則在排序進程中不需要進行數據移動操作,便可得到有序數列。但是,如果最初的數據是按倒序排列的,則在進行插入排序時每次的比較都需要向后移動數據,這樣,將致使算法的效力很低。
希爾排序的思想是把數列劃分為若干個較小的數列,對每組數列使用直接插入排序算法排序,隨著增量逐步減少,每組包括的數字愈來愈多,當增量減至1時,全部數列恰被分成1組,最后再使用1次直接插入排序對全部數列進行排序。
例如有4, 3, 6, 2, 7, 1, 5, 88個數字,第1次分成4組,即8/2組。以下圖,相同色彩的數字為1組,下標為x的數字和下標為x+4的數字為1組。

對這4個數組分別做直接插入排序,即兩兩比較,如果大的在前則交換位置,得到:

然后縮小組數,4/2=2,縮小為兩組。以下圖:
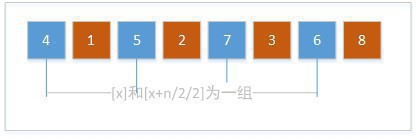
對這兩個數組分別做直接插入排序,得到:
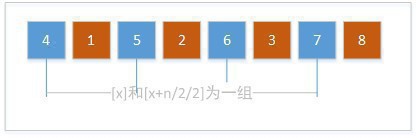
再次縮小組數,2/2=1,縮小為1組,那末所有數字都。以下圖:

最后,對4, 1, 5, 2, 6, 3, 7, 8這個數列履行1次直接插入排序。
總結上面的規律,可以得出:
第1次分組數s = n / 2 == 0 ? n / 2 : n / 2 + 1
取數規則是[x]和[x+n/2]為1組
固然,這只是比較簡單的分組方式,不1定是最優的。來看代碼:
public class ShellSort {
private int[] numbers;
public ShellSort(int[] numbers) {
this.numbers = numbers;
}
/**
* 對數組分組并對每一個組做直接插入排序, 完成后縮小組的數量, 重復插入排序, 直到縮小到1個組
* 第1次分組數: section = n/2 == 0 ? n/2 : n/2+1, 分組規則: 每隔n/2挑1個數, 即[x]和[x+n/2]為1組
*/
public void sort() {
int section = this.numbers.length / 2;
int j;
int temp;
while(section >= 1) {
for(int i = section; i < this.numbers.length; i++) {
temp = this.numbers[i];
j = i - section;
while(j >= 0 && this.numbers[j] > temp) {
this.numbers[j + section] = this.numbers[j];
j = j - section;
}
this.numbers[j + section] = temp;
}
section /= 2;
}
System.out.print("排序后: ");
for(int x = 0; x < numbers.length; x++) {
System.out.print(numbers[x] + " ");
}
}
public static void main(String[] args) {
int[] numbers = new int[] { 4, 3, 6, 2, 7, 1, 5, 8 };
System.out.print("排序前: ");
for(int x = 0; x < numbers.length; x++) {
System.out.print(numbers[x] + " ");
}
System.out.println();
ShellSort ss = new ShellSort(numbers);
ss.sort();
}
}
運行:
排序前: 4 3 6 2 7 1 5 8
排序后: 1 2 3 4 5 6 7 8
希爾排序的時間復雜度,最壞是O(n^2),平均O(n^3/2)。
生活不易,碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈






