ArcGIS教程：根據經驗半變異函數擬合模型

　　半變異函數/協方差建模是空間描寫和空間預測之間的關鍵步驟。地統計的主要利用是預測未采樣位置處的屬性值(克里金法)。

　　經驗半變異函數和協方差可提供有關數據集的空間自相干的信息。但是，不提供所有可能方向和距離的信息。因此，為確保克里金法預測的克里金法方差為正值，根據經驗半變異函數/協方差擬合模型(即連續函數或曲線)是很有必要的。

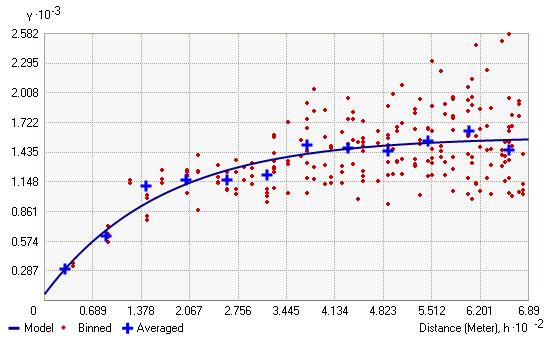
　　經驗半變異函數/協方差值的不同視圖

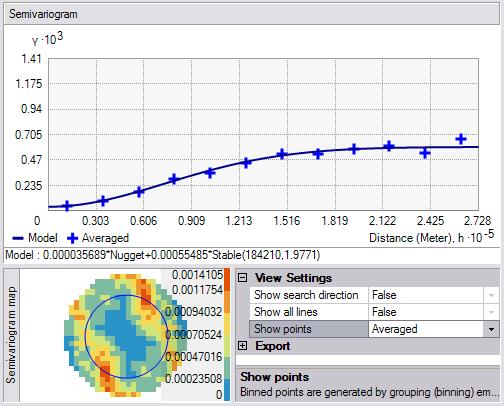
　　地統計向導可提供經驗半變異函數值的3種不同視圖。可使用任意數量(1個、兩個或全部3個)的視圖來幫助您根據數據擬合模型。默許視圖顯示了已拋棄和已平均化的經驗半變異函數/協方差值。

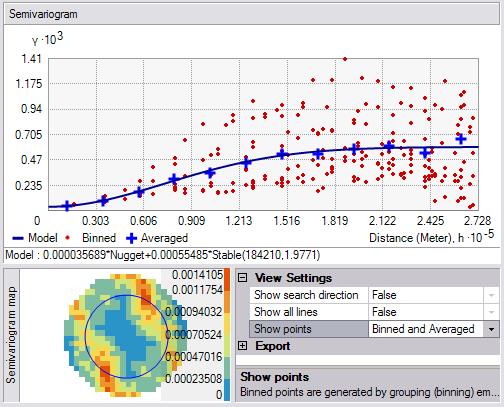
　　已拋棄值顯示為紅色的點，是通過使用寬為1個步長的方形像元將經驗半變異函數/協方差點組合(分組)在1起后生成的。平均點顯示為藍色的10字符號，是通過將處于圓周分區內的經驗半變異函數/協方差點進行分組后生成的。拋棄點顯示半變異函數/協方差值中的局部變化，而平均值顯示半變異函數/協方差值的平滑變化。在很多情況下，根據平均值擬合模型會更容易1些，由于它們將為數據中的空間自相干提供相對簡潔的視圖，與拋棄點相比，平均值將顯示的半變異函數值的變化更加平滑。

　　顯示點控件可以設置為“已拋棄和已平均化”(如上圖所示)、“已拋棄”或“已平均化”(以下圖所示)。

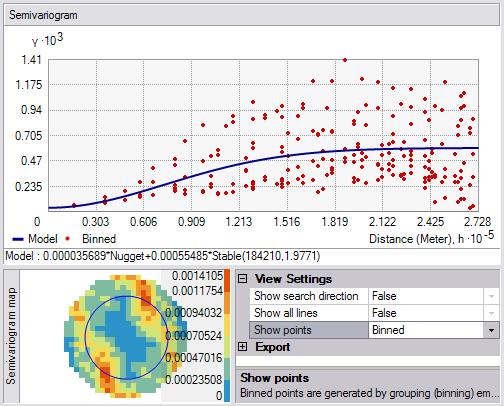
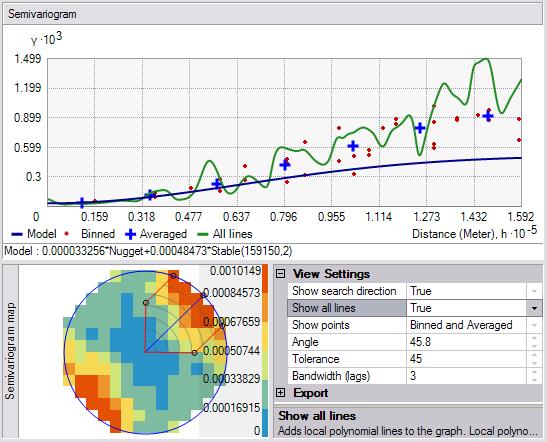
　　另外，還可以向圖中添加線。這些線是根據已拋棄的經驗半變異函數/協方差值進行擬合的局部多項式。如果將顯示搜索方向選項設置為 True，則只會顯示根據“顯示搜索方向”工具的中軸樣帶中經驗半變異函數/協方差表面擬合的局部多項式，以下圖所示：

　　根據經驗數據擬合的半變異函數/協方差模型應當：

• 　　穿過已拋棄值(紅色的點)云的中心。
• 　　穿過盡量接近平均值(藍色的10字符號)的位置。
• 　　穿過盡量接近線(綠色的線)的位置。

　　請記住，即便模型沒有完全擬合經驗數據，您對現象的認識也能夠決定模型的形狀和塊金和變程值、偏基臺值和各向異性值(回想1下，經驗數據只是要構建的真實現象模型的樣本，其實不能完全代表真實現象的所有空間和統計方面)。

　　不同類型的半變異函數/協方差模型

　　Geostatistical Analyst 為構建經驗半變異函數模型提供以下函數：

• 　　圓
• 　　球面
• 　　4球
• 　　5球
• 　　指數
• 　　高斯
• 　　有理2次方程式
• 　　孔洞效應
• 　　K-Bessel
• 　　J-Bessel
• 　　穩定的

　　所選模型會影響未知值的預測，特別是當接近原點的曲線形狀明顯不同時。接近原點處的曲線越陡，最接近的相鄰元素對預測的影響就越大。

　　這樣，輸出曲面將更不平滑。每一個模型都用于更準確地擬合不同種類的現象。

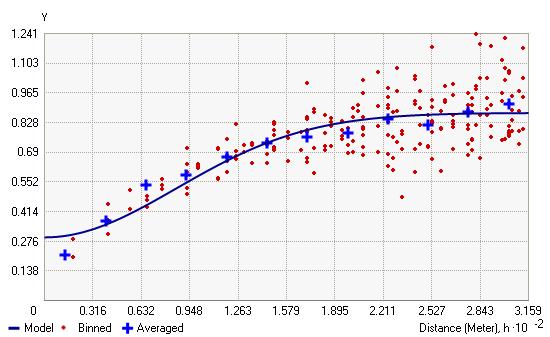
　　下圖顯示了兩個經常使用模型(“指數”和“高斯”)并標識了函數的不同的地方：

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈