Coursera Machine Learning 學(xué)習(xí)筆記（八）

IV. Linear Regression with Multiple Variables (Week 2)

- Multiple features

       之前我們介紹了單變量/單特點的回歸模型，現(xiàn)在我們對房價預(yù)測模型增加更多的變量也就是更多的特點，比如房間數(shù)、樓層、房齡等，從而構(gòu)成1個含有多個變量/特點的模型。

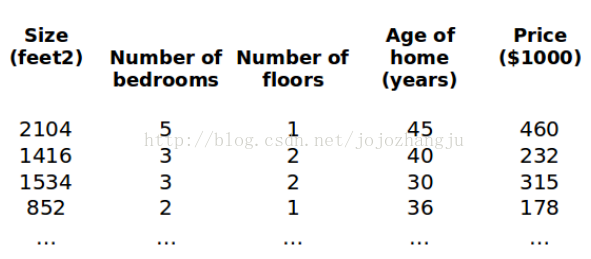
       在增加了更多變量/特點以后，我們將引入1系列新的符號和解釋：

       n 代表變量/特點的個數(shù) 

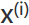       代表第i個訓(xùn)練實例，也就是特點矩陣中的第i行，即1個向量

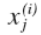       代表第i個訓(xùn)練實例的第j個特點，也就是特點矩陣中第i行的第j個特點

       因此，多變量/特點的假定h可以表示為：

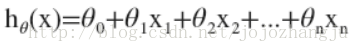
       這個公式中有n+1個參數(shù)和n個變量，為了簡化公式，我們令，則公式則表示為：

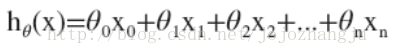
       此時h中的參數(shù)是1個n+1維的向量，訓(xùn)練實例也都是n+1維的向量。

       因此公式可以簡化為：

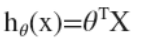
       其中上標(biāo)T代表了矩陣的轉(zhuǎn)置。

- Gradient descent for multiple variables

       與單變量/特點線性回歸相似，在多變量/特點線性回歸中，我們也將定義1個代價函數(shù)，即：

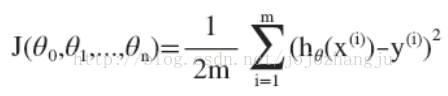
       我們的目標(biāo)和單變量/特點線性回歸中的問題相同，就是要找出使得代價函數(shù)最小的參數(shù)組合。

       因此，多變量/線性回歸梯度降落算法為：

       即：

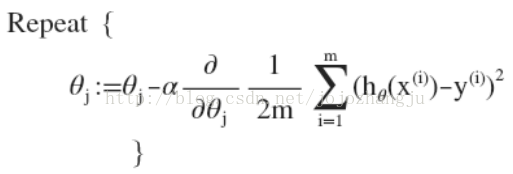
       求導(dǎo)數(shù)后可以得到：

       以后，我們通過隨機(jī)更新1系列的值并計算代價函數(shù)，直到收斂。

生活不易，碼農(nóng)辛苦
如果您覺得本網(wǎng)站對您的學(xué)習(xí)有所幫助,可以手機(jī)掃描二維碼進(jìn)行捐贈