【機器學習基礎】驗證

模型選擇問題(Model Selection Problem)

我們在之前得知，通過最小化Ein來選擇最好的模型不是1個正確的辦法，由于這樣可能會付出模型復雜度的代價、造成泛化效果差、造成過擬合的產生。
為了解決這個問題，我們的想法是找1些測試數據來看看哪一種模型對應測試數據的效果更好，但是用新的測試數據來作這個事情，實際上是做不到的掩耳盜鈴的辦法。
我們對照這兩種方式，用訓練數據來作選擇的話，由于這些數據決定了終究的假定，所以再用這些訓練數據來作驗證的時候已被“污染”了；而如果用新的數據對測實驗證的來講，是“清潔”的。
折衷的辦法是，將可用的數據留1小部份作為驗證數據，當作模型選擇的時候，再拿來用于驗證。

驗證

現在，我們從手中的數據拿出1小部份出來作驗證數據，我們拿它來摹擬測試數據。為了將針對驗證數據的毛病Eval和Eout聯系起來，我們希望數據獨立同散布于原始數據的散布；剩下的數據用作訓練數據，可以用來做模型選擇。

使用最好的Eval做模型選擇

在做模型選擇時，我們遵守以下流程，首先將數據集D分成兩部份Dtrain和Dval，用Dtrain算出不同假定Hi的g-，再用Dval算出Ei，我們得到最小的Ei（記為Em）和其對應的假定Hm，再將所有的數據放在1起用Hm這個模型算出終究的模型參數gm（這個gm是用了最好的模型和最多的數據算出的結果，這會使得Eout最小）。

關系圖形

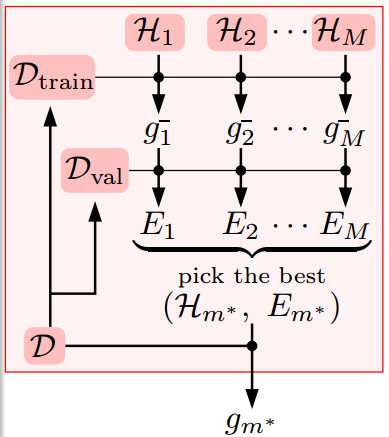
我們用1個圖形關系來表示不同的驗證數據對真實誤差Eout的影響。

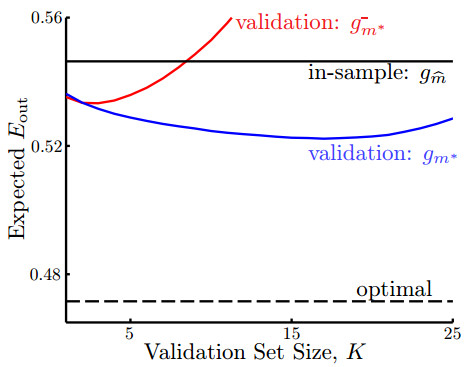
上面這個圖的橫軸是驗證數據的大小是多少，縱軸表示Eout的大小。
其中紅色的線代表用驗證數據得到的終究假定g-，該假定不再用所有的數據重新做1次訓練。
藍色的線代表用驗證數據得到了g-以后，在拿訓練數據和驗證數據放在1起做1次訓練，得到的g。
不言而喻的是，藍色的線總是比紅色的線要低，并且藍色的線比黑色的橫線（表示直接用所有數據做訓練得到的Ein）要低（這表示用驗證數據得到的假定真的比不用驗證數據得到的假定的誤差要低）。
這說明，驗證這個步驟確切是1個有用的方法。

那末為何紅色的線有時候比Ein得到的g的毛病要大呢？
其解釋是，如果驗證數據變大，訓練數據變小時，g-是用比較少的數據求出來的，所以g-的表現是不好的。用很少的數據選取的最好的g-有可能比起用全部數據訓練得到的g還要差。

驗證數據的大小

我們的決策根植于1個假定，我們要得到最后的假定g，所以希望Eout(g)和用驗證數據得到Eout(g-)接近，另外還希望Eout(g-)和Eval(g-)接近。我們用Eval(g-)做選擇，最后希望得到Eout(g)最好的那個假定。

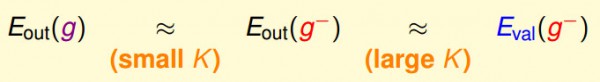
這兩個近似等式需要的驗證數據的數量是不同的，Eout(g-)≈Eval(g-)需要更多的驗證數據，但這樣會造成g-和g差很多（即上面的關系圖形中，紅色和藍色的線在驗證數據多的時候會差別很大）；Eout(g)≈Eout(g-)需要數量少的驗證數據，但這是不太能肯定Eval和Eout是否是接近的。
實際上，驗證數據量K=N/5，其中N是訓練數據。

留1交叉驗證

如果只有1個數據來作驗證的話，那末其毛病Eval是：

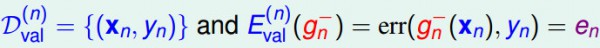
如果將所有的數據都拿來作驗證的話，將其得到的結果平均起來，大概就可以告知我們Eout的情況：

理論保證

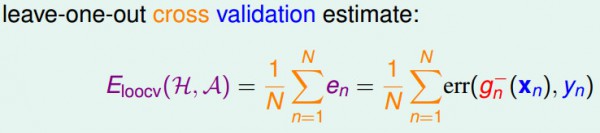
我們現在從偏理論的角度解釋留1交叉檢驗的誤差期望值和Eout(g-)的近似關系。
首先，我們假定對各式各樣不同的數據集來作交叉檢驗并取1個平均。這里表示的都是leave-one-out交叉檢驗誤差的期望值和Eout(g-)的期望值是差不多的。

實際利用

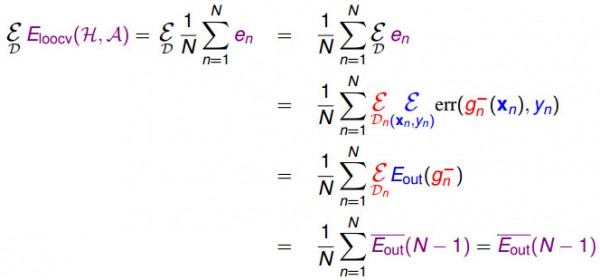
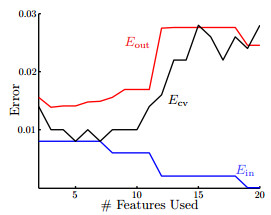
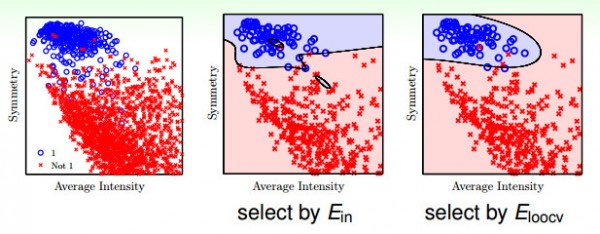
下圖的橫軸是特點轉換的維度，從圖中可以看出來，如果拿Ein來作選擇，用盡可能多的特點可以做到盡量小的Ein，但是釀成的結果是過擬合，所以如果用較少的特點，Eout可能還小1點；如果用交叉檢驗的Ecv來作選擇，其曲線和Eout的曲線很接近，所以就想下面第2個圖中最右邊的圖象表示的，雖然會有1些錯分類的情形，但是分類的曲線平滑很多，其在實際的表現就會更好。
這說明使用交叉驗證的方法求得的假定可以比Ein得到的效果更好。

可能的問題

如果有1000個數據，我們用leave-one-out來作交叉驗證的話，就需要做1000次來得到平均的誤差，這樣比較耗時，不太實際。

V折交叉檢驗

在留1交叉檢驗中，我們取1份數據來作驗證，其余數據來作訓練，
為了簡單起見，我們可以將數據切成10部份，然后拿其中9份做訓練，另外1份做驗證，這樣和留意交叉檢驗的效果是類似的。

常見的方式是將數據分成10份。
這類V折的交叉驗證的方式比單1驗證的方式更加穩定。

轉載請注明作者Jason Ding及其出處
Github博客主頁(http://jasonding1354.github.io/)
CSDN博客(http://blog.csdn.net/jasonding1354)
簡書主頁(http://www.jianshu.com/users/2bd9b48f6ea8/latest_articles)

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈