以下是關于2D的1些理論和推導進程,詳細描寫了圖象的平移、縮放和旋轉等;
This article is from: 2D Transformations
Transformaions are a fundamental part of computer graphics. Transformations are used to position objects, to shape objects, to change viewing positions, and even to change how something is viewed (e.g. the type of perspective that is used).


In 3D graphics, we must use 3D transformations. However, 3D transformations can be quite confusing so it helps to first start with 2D.
There are 4 main types of transformations that one can perform in 2 dimensions:
These basic transformations can also be combined to obtain more complex transformations. In order to make the representation of these complex transformations easier to understand and more efficient, we introduce the idea of homogeneous coordinates.
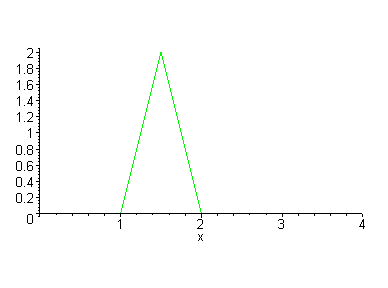
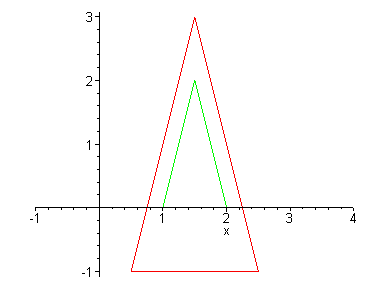
A point p in 2D is represented as a pair of numbers: p= (x, y) where x is the x-coordinate of the point p and y is the y-coordinate of p . 2D objects are often represented as a set of points (vertices), {p1,p2,...,pn}, and an associated set of edges {e1,e2,...,em}. An edge is defined as a pair of points e = {pi,pj}. What are the points and edges of the triangle below?
We can also write points in vector/matrix notation as
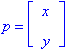
Assume you are given a point at (x,y)=(2,1). Where will the point be if you move it 3 units to the right and 1 unit up? Ans: (x',y') = (5,2). How was this obtained? - (x',y') = (x+3,y+1). That is, to move a point by some amount dx to the right and dy up, you must add dx to the x-coordinate and add dy to the y-coordinate.
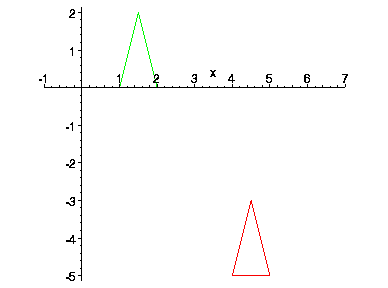
What was the required transformation to move the green triangle to the red triangle? Here the green triangle is represented by 3 points
triangle = { p1=(1,0), p2=(2,0), p3=(1.5,2) }
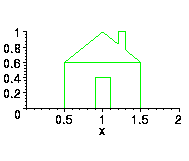
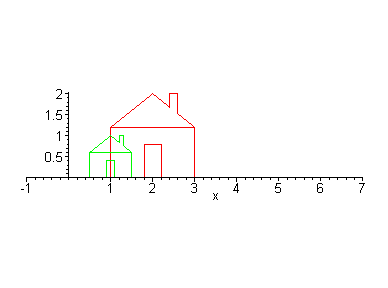
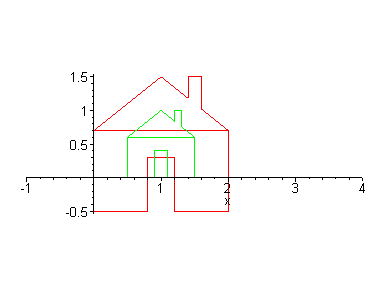
What are the points and edges in this picture of a house? What are the transformation is required to move this house so that the peak of the roof is at the origin? What is required to move the house as shown in animation?
 click
here for animation
click
here for animation
Matrix/Vector Representation of Translations
A translation can also be represented by a pair of numbers, t=(tx,ty) where tx is the change in the x-coordinate and ty is the change in y coordinate. To translate the point p by t, we simply add to obtain the new (translated) point q = p + t.
q = p + t = 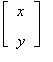 +
+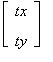 =
= 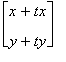
Suppose we want to double the size of a 2-D object. What do we mean by double? Double in size, width only, height only, along some line only? When we talk about scaling we usually mean some amount of scaling along each dimension. That is, we must specify how much to change the size along each dimension. Below we see a triangle and a house that have been doubled in both width and height (note, the area is more than doubled).
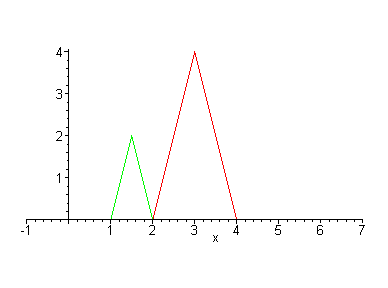
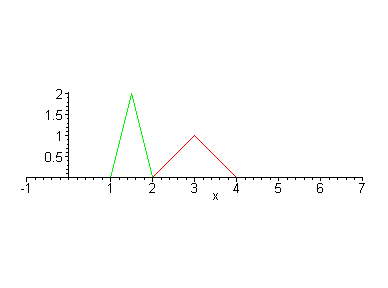
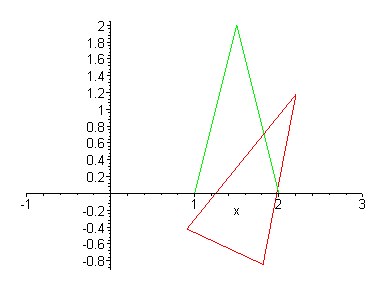
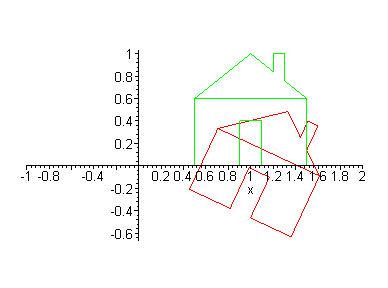
The scaling for the x dimension does not have to be the same as the y dimension. If these are different, then the object is distorted. What is the scaling in each dimension of the pictures below?
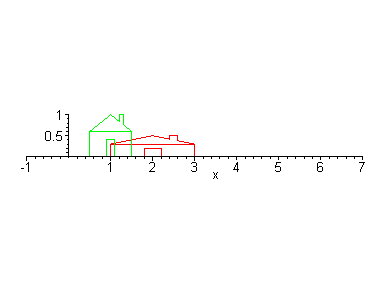
And if we double the size, where is the resulting object? In the pictures above, the scaled object is always shifted to the right. This is because it is scaled with respect to the origin. That is, the point at the origin is left fixed. Thus scaling by more than 1 moves the object away from the origin and scaling of less than 1 moves the object toward the origin. This can be seen in the animation below.
 click
here for animation
click
here for animation
This is because of how basic scaling is done. The above objects have been scaled simply by multiplying each of its points by the appropriate scaling factor. For example, the point p=(1.5,2) has been scaled by 2 along x and .5 along y. Thus, the new point is
q = (2*1.5,.5*2) = (3,1).
Matrix/Vector Representation of Translations
Scaling transformations are represented by matrices. For example, the above scaling of 2 and .5 is represented as a matrix:
scale matrix: s = 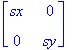 =
= 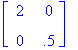
new point: q = s*p = 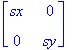
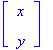 =
= 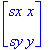
Scaling about a Particular Point
What do we do if we want to scale the objects about their center as show below? Answer
Below, we see objects that have been rotate by 25 degrees.
Again, we see that basic rotations are with respect to the origin:
 click
here for animation
click
here for animation
Matrix/Vector Representation of Translations
counterclockwise rotation of a degrees = 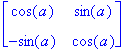
 click
here for animation
click
here for animation
Matrix/Vector Representation of Translations
shear along x axis = 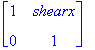
shear along y axis = 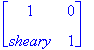
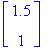
We saw that the basic scaling and rotating transformations are always with respect to the origin. To scale or rotate about a particular point (the fixed point) we must first translate the object so that the fixed point is at the origin. We then perform the scaling or rotation and then the inverse of the original translation to move the fixed point back to its original position. For example, if we want to scale the triangle by 2 in each direction about the point fp = (1.5,1), we first translate all the points of the triangle by T = (⑴.5,⑴), scale by 2 (S) , and then translate back by -T=(1.5,1). Mathematically this looks like
q = 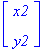 =
= 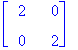 (
( 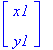 +
+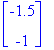 ) +
) + 
Notice the order in which these transformations are performed. The first (rightmost) transformation is T and the last (leftmost) is -T. If you apply these transformations in a different order then you will get very different results. For example, what happens when you first apply T followed by -T followed by S? Here T and -T cancel each other out and you are simply left with S
.Sometimes (but be careful) order does not matter, For example, if you apply multiple 2D rotations, order makes no difference:
R1 R2 = R2 R1
But this will not necessarily be true in 3D!!
In general, when you want to perform a complex transformation, you usually make it by combining a number of basic transformations. The above equation for q, however, is awkward to read because scaling is done by matrix multiplication and translation is done by vector addition. In order to represent all transformations in the same form, computer scientists have devised what are called homogeneous coordinates. Do not try to apply any exotic interpretation to them. They are simply a mathematical trick to make the representation be more consistent and easier to use.
Homogeneous coordinates (HC) add an extra virtual dimension. Thus 2D HC are actually 3D and 3D HC are 4D. Consider a 2D point p = (x,y). In HC, we represent p as p = (x,y,1). An extra coordinate is added whose value is always 1. This may seem odd but it allows
us to now represent translations as matrix multiplication instead of as vector addition. A translation (dx, dy) which would normally be performed as q = (x,y) + (dx, dy) now is written as
q = T p = 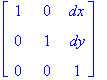
 =
= 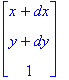
Now, we can write the scaling about a fixed point as simply a matrix multiplication:
q = (-T) S T p = A p,
where A = (-T) S T
The matrix A can be calculated once and then applied to all the points in the object. This is much more efficient than our previous representation. It is also easier to identify the transformations and their order when everything is in the form of matrix multiplication.
The matrix for scaling in HC is
S = 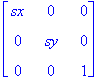
and the matrix for rotation is
R = 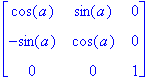

下一篇 CSS布局基礎匯總