第9章

• 前言
• 甚么是卷積
• 神經網絡里卷積的目的
• 甚么是池化
• 卷積和池化的強先驗

前言

卷積網絡也叫卷積神經網絡（或CNN），是1種特殊的深層的神經網絡模型，它合適于時間序列數據的處理和圖象數據處理。

這章內容主要討論內容：

• 甚么是卷積
• 使用卷積的動機
• 甚么是池化
• 用于實踐中的神經網絡的幾個變化卷積函數
• 卷積如何利用于各種維度不同的數據
• 討論1些如何使卷積神經更有效力

補充內容：

卷積神經網絡的特殊性體現在兩個方面，1方面它的神經元間的連接是非全連接的， 另外一方面同1層中某些神經元之間的連接的權重同享的（即相同的）。它的非全連接和權值同享的網絡結構使之更類似于生物神經網絡，下降了網絡模型的復雜度（對很難學習的深層結構來講，這是非常重要的），減少了權值的數量。

9.1卷積運算

卷積運算是通過兩個函數f$f$和g$g$ 生成第3個函數的1種數學算子，表征函數f$f$與g$g$經過翻轉和平移的堆疊部份的面積。（百度百科）

為了說明卷積運算，我們1個通過激光傳感器來定位飛船位置的例子。
x(t)$x(t)$：激光傳感器的輸出
t$t$:某個時刻，這2個 變量都是實數

假定:激光傳感器有1定的噪聲，為了取得較小的噪聲，我們采取了幾種丈量方式，越新的測試方法，越可靠，所以我們給定比較新的丈量方法，更大的權重。我們得到權重函數：w(a)$w(a)$，變量a$a$是丈量的年代。如果我們將這個函數利用到每個時刻，我們的得到了1個新的函數：
s(t)=∫x(a)w(t?a)da$s(t) = \int x(a)w(t ? a)da$

這個操作叫卷積，通常卷積定義為：s(t)=(x?w)(t)$s(t) = (x ? w)(t)$

w$w$代表幾率密度函數，或帶有權重的均值。對卷積函數第1個函數x$x$，被稱作輸入，第2個w$w$，被稱作核函數。如果激光傳感器每秒丈量1次，t$t$就是1個整數集合。s(t)=(x?w)(t)=∑a=?∞∞x(a)w(t?a)$\displaystyle s(t) = (x ? w)(t) =\sum _{a=-\infty}^{\infty}x(a)w(t-a)$
我們常常會用卷積操作1個多坐標數據，比如我們用1個2維的圖片作為輸入，一樣用2維的核K$K$：

S(i,j)=(I?K)(i,j)=∑m∑nI(m,n)K(i?m)(j?n)$\displaystyle S(i,j) = (I * K)(i,j) = \sum_m \sum_n I(m,n)K(i-m)(j-n)$

卷積的可計算性，我們可以等效的寫成：
S(i,j)=(K?I)(i,j)=∑m∑nI(i?m,j?n)K(m)(n)$\displaystyle S(i,j) = (K * I)(i,j) = \sum_m \sum_n I(i-m,j-n)K(m)(n)$

卷積運算的交換律的出現，是由于我們可以翻轉核函數和輸入值。很多深度學習庫，都實現了相互關的函數。它和卷積是1樣的，不過沒有翻轉核函數。
S(i,j)=(I?K)(i,j)=∑m∑nI(i+m,j+n)K(m)(n)$\displaystyle S(i,j) = (I * K)(i,j) = \sum_m \sum_n I(i+m,j+n)K(m)(n)$
1個基于核翻轉卷積算法將學習到相不翻轉內核無需翻轉由算法學到的內核。這也是很難看到單獨使用卷積到機器學習;卷積1般和其他算法組合使用，這些組合函數不管使用翻轉核卷積運算還是非翻轉核卷積運算都不再變換。

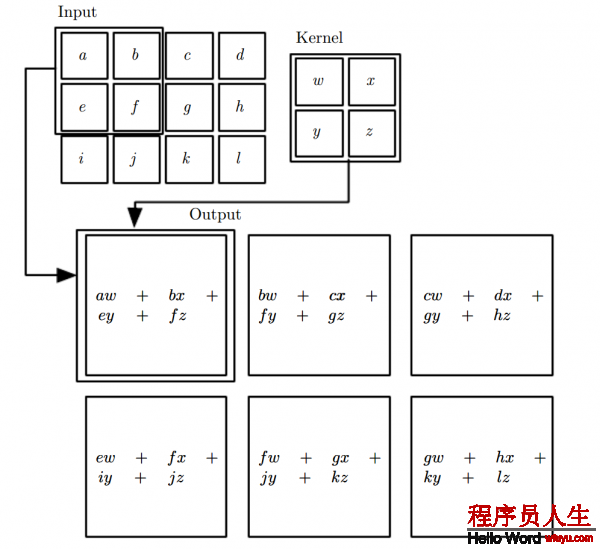
圖9.1：非核翻轉2-D卷積的1個例子。在這類情況下，我們限制輸出的位置，其中核數據完全位于圖象內，在某些情況下，被稱為有效卷積。我們用正方形上的箭頭唆使左上角輸入矩陣數據的元素通過施加右上角輸入矩陣的區域的核數據，進行1個相互關計算。

9.2使用卷積的動機

卷積充分利用3個重要觀點來改良深度學習系統：稀疏連接，參數同享和等效表示。另外，卷積提供了1種方法，來處理可變長的輸入數據。傳統的神經網絡使用每個參數矩陣和輸入矩陣相乘，算出輸出值，這意味著每一個輸出單元和輸入單元都相互作用。卷積網絡是稀疏連接的，這個是通過1個比輸入小的核來實現的。比如，當處理圖象時，這個輸入圖片，有成千或百萬像素，但我們可以檢測到1些小的有用的特點，比如核占據的幾10或上百的像素的1些邊沿。這意味著我們只需要保存更少的參數，這樣可以下降模型所需內存，改良它的統計效力。如果存在1個m維的輸入數據，和n維的輸出數據，那末矩陣相乘需
要m×n$m × n$個參數，算法需要1個O(m×n)$O(m × n)$復雜度。如果我們限制輸出層的鏈接個數為k$k$，那末僅僅需要O(k×n)$O(k × n)$復雜度。對稀疏連接的圖片展現，可以參考圖9.2和圖9.3.在卷積神經網絡里， 隱含層單元沒必要直接和每個輸入層神經單元互聯，如圖9.4。

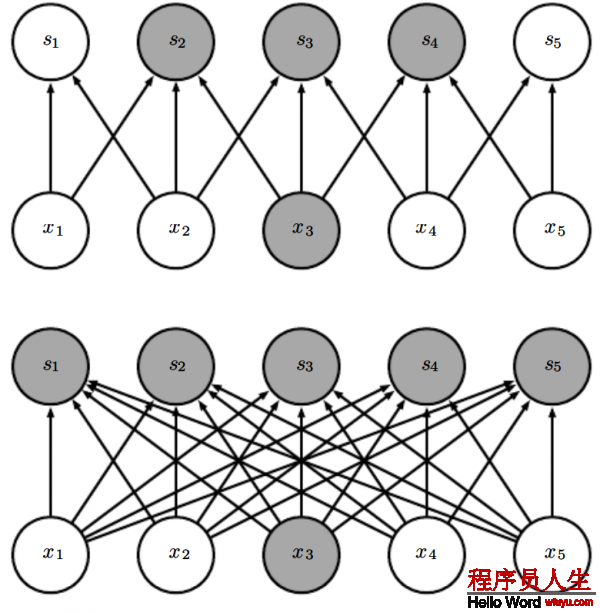
圖9.2：稀疏連接，從圖片的下臉部分可知：我們高亮了輸入單元x3$x3$,也高亮了受輸入單元x3$x3$影響的輸出單元，只有3個輸出單元受它影響。（圖底部）當s$s$是由矩陣相乘得到，那末連接性不再是稀疏的，所有的輸出單元都遭到它的影響。

圖9.3

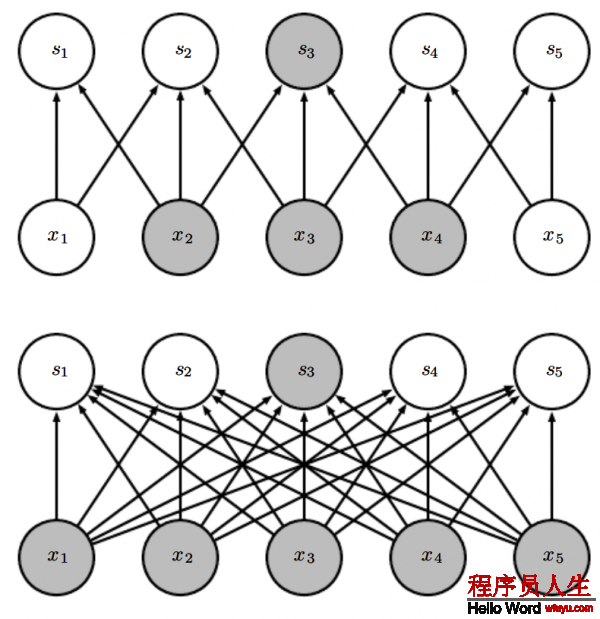
圖9.4

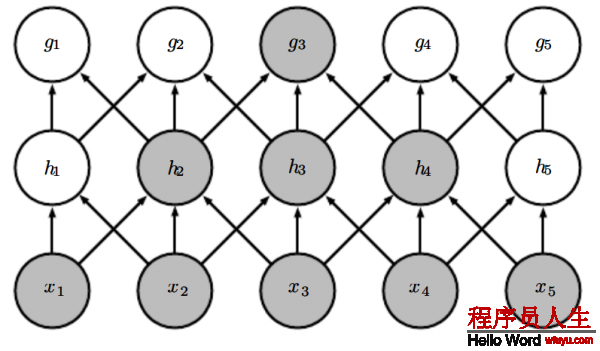
圖9.4：卷積神經網絡里的深層神經單元的感知野比淺層神經元的感知野要大很多，如果神經網絡里加入1些像步長卷積或池化，那末這個效果會增強。這意味著即便即便在在卷積神經網絡里進行全連接,也會變得稀疏，在深層的神經元可以不和所有或大多數輸入神經元連接。
參數同享是指在模型中的多個函數同享相同的參數。在傳統的神經網絡里，在計算輸出層時候，權重矩陣的每個元素都會被計算1次，然后就不再使用。至于參數同享的代名詞，也能夠說，網絡連接權重，由于既然權值可以利用到1個輸入單元上，那末就能夠利用到任何地方。在卷積神經網絡，核中的每一個元素都被利用到輸入數據的每一個元素中（除也許有些邊界像素，這取決于邊界的設計決策）。通過卷積運算使用的參數的同享意味著我們不是在每個位置上都學習1組獨立的參數，而是我們只學1組參數。這不會影響前向反饋算法-它依然是O(k×n)$O(k × n)$存儲空間，但是它進1步減少了模型的存儲需求。回想當k$k$通常是遠遠小于m$m$幾個數量級。
由于m$m$和n$n$通常大小大致相同，k$k$與M×N$M×N$相比是幾近微不足道。卷積因此和密度矩陣乘法相比，在內存使用和統計效力方面更高效，為描寫參數同享是如何工作的,參見圖9.5.

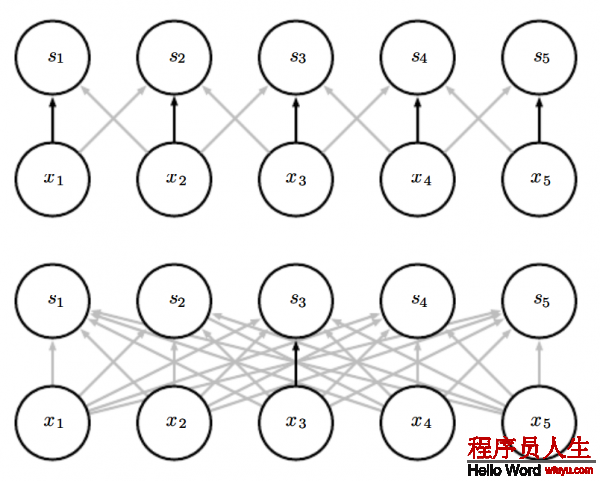
圖 9.5:
權值同享:黑色箭頭表示用某個特定的參數來連接2個不同模型。（上面）黑色箭頭表示在卷積神經模型里我們使用3個核元素中的中間那個元素。由于權重同享這個參數被所有的輸入單元使用。（下面）單個那個黑色箭頭表明權值矩陣的中間那個元素在1個全連接的網絡模型中被使用。這個模型里參數沒有被同享只是被使用了1次。

作為1個實戰中利用前2個原理（稀疏連接，參數同享）的1個實例，圖9.6 表明了，稀疏連接，參數同享如何在圖片中檢測邊的線性函數提高了效力。

在卷積時，由于權重同享而產生的1個特性叫轉換等效性,如果說1個函數是等效的，那末意味著在輸入中變化，那末在輸出中也會一樣變化。如果滿足：f(g(x))=g 生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈