動態規劃 最長公共子序列 過程圖解

1.基本概念

      首先需要科普1下，最長公共子序列（longest common sequence）和最長公共子串（longest common substring）不是1回事兒。甚么是子序列呢？即1個給定的序列的子序列，就是將給定序列中零個或多個元素去掉以后得到的結果。甚么是子串呢？給定串中任意個連續的字符組成的子序列稱為該串的子串。給1個圖再解釋1下：

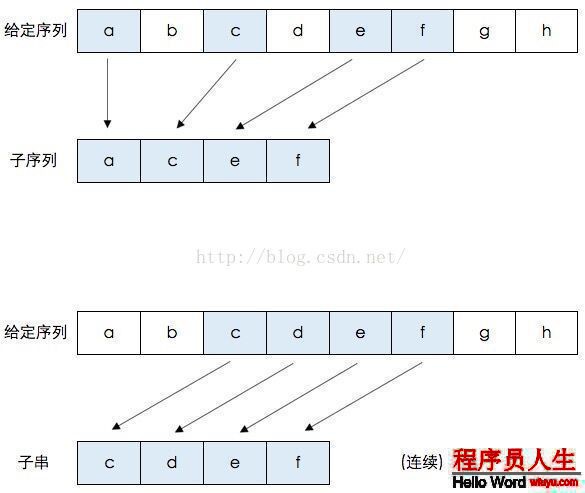
       如上圖，給定的字符序列： {a,b,c,d,e,f,g,h}，它的子序列示例： {a,c,e,f} 即元素b,d,g,h被去掉后，保持原本的元素序列所得到的結果就是子序列。同理，{a,h},{c,d,e}等都是它的子序列。
       它的字串示例：{c,d,e,f} 即連續元素c,d,e,f組成的串是給定序列的字串。同理，{a,b,c,d},{g,h}等都是它的字串。

        這個問題說明白后，最長公共子序列（以下都簡稱LCS）就很好理解了。
給定序列s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}，s1和s2的相同子序列，且該子序列的長度最長，即是LCS。
s1和s2的其中1個最長公共子序列是 {3,4,6,7,8}

2.動態計劃

       求解LCS問題，不能使用暴力搜索方法。1個長度為n的序列具有 2的n次方個子序列，它的時間復雜度是指數階，太恐怖了。解決LCS問題，需要借助動態計劃的思想。
       動態計劃算法通經常使用于求解具有某種最優性質的問題。在這類問題中，可能會有許多可行解。每個解都對應于1個值，我們希望找到具有最優值的解。動態計劃算法與分治法類似，其基本思想也是將待求解問題分解成若干個子問題，先求解子問題，然后從這些子問題的解得到原問題的解。與分治法不同的是，合適于用動態計劃求解的問題，經分解得到子問題常常不是相互獨立的。若用分治法來解這類問題，則分解得到的子問題數目太多，有些子問題被重復計算了很屢次。如果我們能夠保存已解決的子問題的答案，而在需要時再找出已求得的答案，這樣就能夠避免大量的重復計算，節省時間。我們可以用1個表來記錄所有已解的子問題的答案。不管該子問題以后是不是被用到，只要它被計算過，就將其結果填入表中。這就是動態計劃法的基本思路。

3.特點分析

       解決LCS問題，需要把原問題分解成若干個子問題，所以需要刻畫LCS的特點。

       設A=“a0，a1，…，am”，B=“b0，b1，…，bn”，且Z=“z0，z1，…，zk”為它們的最長公共子序列。不難證明有以下性質：
       如果am=bn，則zk=am=bn，且“z0，z1，…，z(k⑴)”是“a0，a1，…，a(m⑴)”和“b0，b1，…，b(n⑴)”的1個最長公共子序列；
       如果am!=bn，則若zk!=am，蘊涵“z0，z1，…，zk”是“a0，a1，…，a(m⑴)”和“b0，b1，…，bn”的1個最長公共子序列；
       如果am!=bn，則若zk!=bn，蘊涵“z0，z1，…，zk”是“a0，a1，…，am”和“b0，b1，…，b(n⑴)”的1個最長公共子序列。

       有些同學，1看性質就容易暈菜，所以我給出1個圖來讓這些同學理解1下：

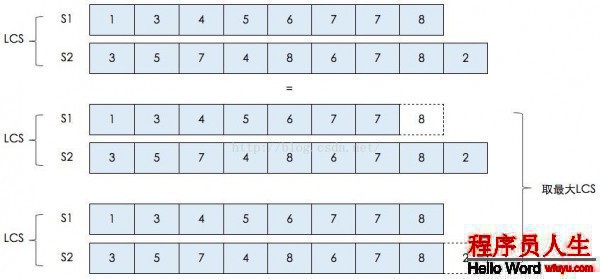
       以我在第1小節舉的例子（S1={1,3,4,5,6,7,7,8}和S2={3,5,7,4,8,6,7,8,2}），并結合上圖來講：

       假設S1的最后1個元素 與 S2的最后1個元素相等，那末S1和S2的LCS就等于 {S1減去最后1個元素} 與 {S2減去最后1個元素} 的 LCS  再加上 S1和S2相等的最后1個元素。

       假設S1的最后1個元素 與 S2的最后1個元素不等（本例子就是屬于這類情況），那末S1和S2的LCS就等于 ： {S1減去最后1個元素} 與 S2 的LCS， {S2減去最后1個元素} 與 S1 的LCS 中的最大的那個序列。

4.遞歸公式

        第3節說了LCS的特點，我們可以發現，假定我需要求 a1 ... am 和 b1 .. b(n⑴)的LCS 和 a1 ... a(m⑴) 和 b1 .. bn的LCS，1定會遞歸地并且重復地把如a1... a(m⑴) 與 b1 ... b(n⑴) 的 LCS 計算幾次。所以我們需要1個數據結構來記錄中間結果，避免重復計算。

        假定我們用c[i,j]表示Xi 和 Yj 的LCS的長度（直接保存最長公共子序列的中間結果不現實，需要先借助LCS的長度）。其中X = {x1 ... xm}，Y ={y1...yn}，Xi = {x1 ... xi}，Yj={y1... yj}。可得遞歸公式以下：

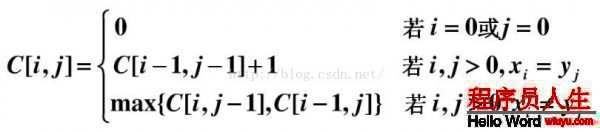
5.計算LCS的長度

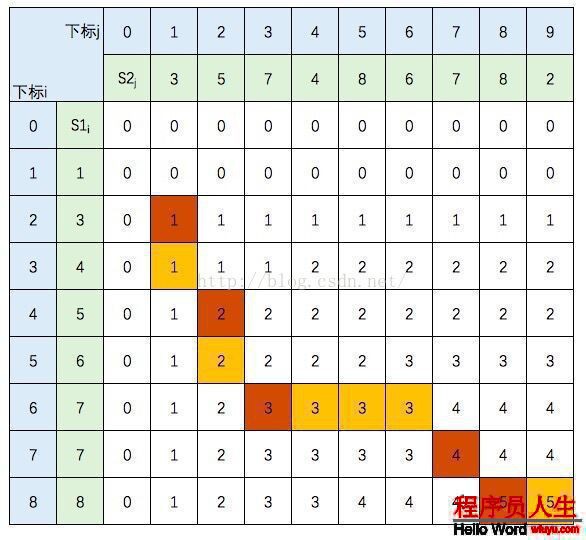
       這里我不打算貼出相應的代碼，只想把這個進程說明白。還是以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}為例。我們借用《算法導論》中的推導圖：

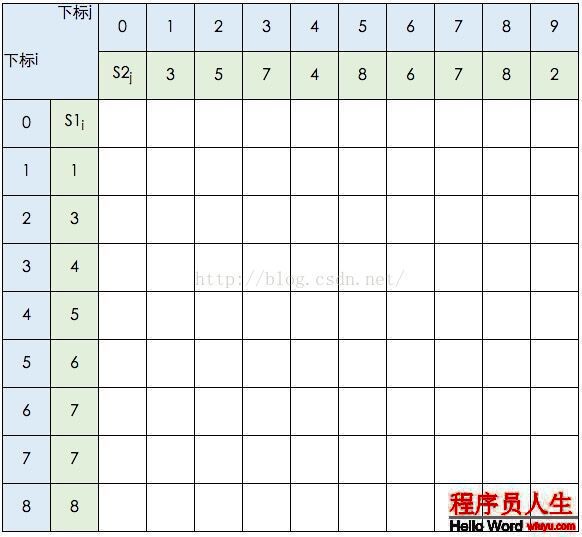
         圖中的空白格子需要填上相應的數字（這個數字就是c[i,j]的定義，記錄的LCS的長度值）。填的規則根據遞歸公式，簡單來講：如果橫豎（i,j）對應的兩個元素相等，該格子的值 = c[i⑴,j⑴] + 1。如果不等，取c[i⑴,j] 和 c[i,j⑴]的最大值。首先初始化該表：

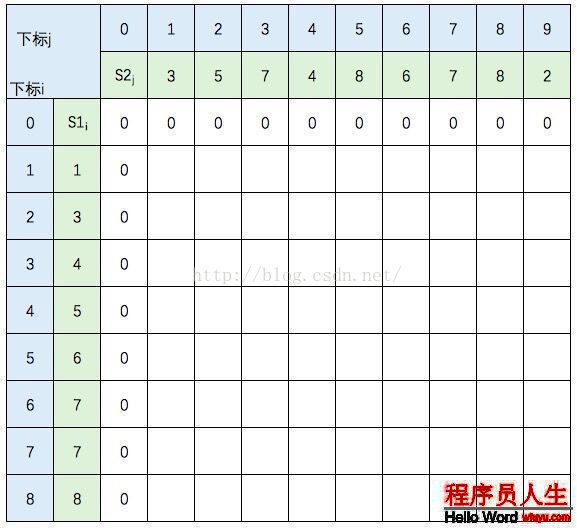
          然后，1行1行地從上往下填：

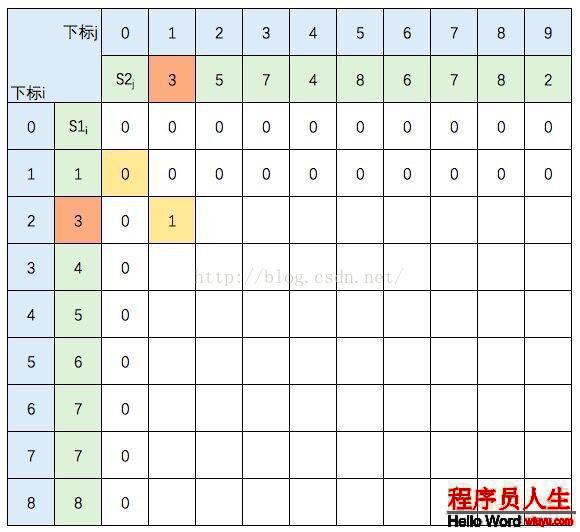
          S1的元素3 與 S2的元素3 相等，所以 c[2,1] = c[1,0] + 1。繼續填充：

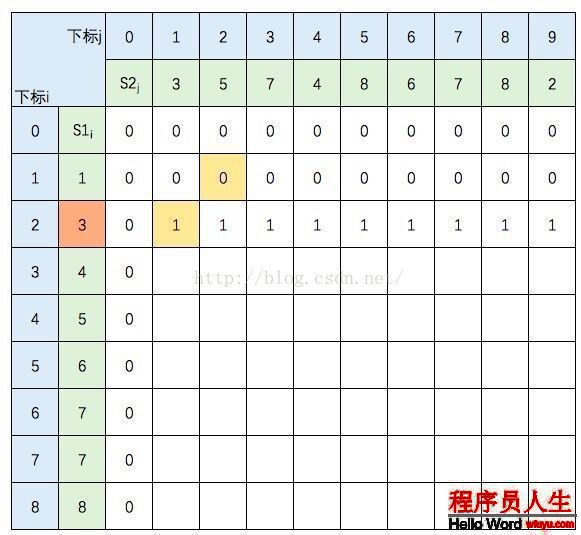
            S1的元素3 與 S2的元素5 不等，c[2,2] =max(c[1,2],c[2,1])，圖中c[1,2] 和 c[2,1] 背風景為淺黃色。

            繼續填充：

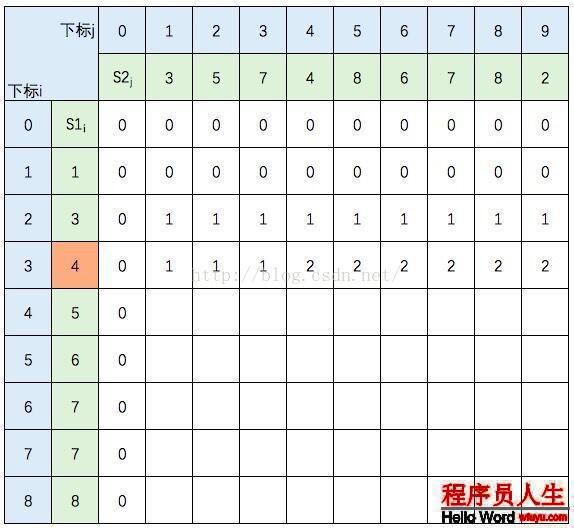
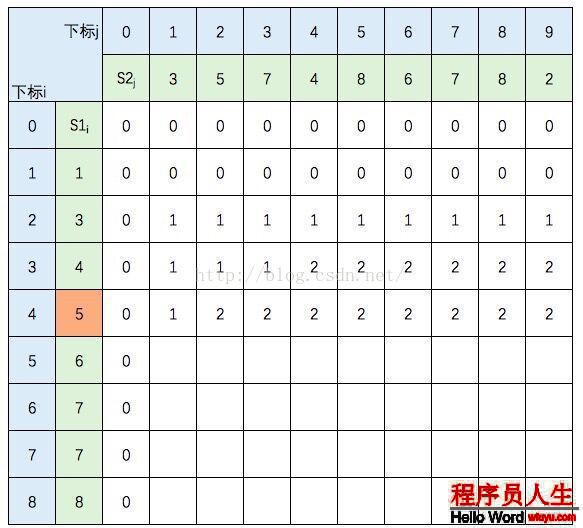
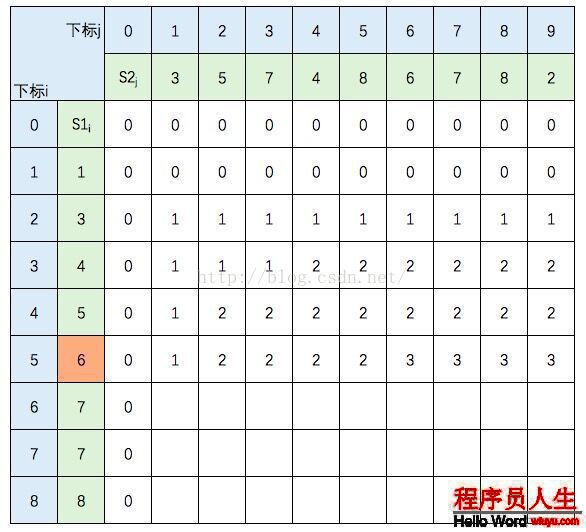
               中間幾行填寫規則不變，直接跳到最后1行：

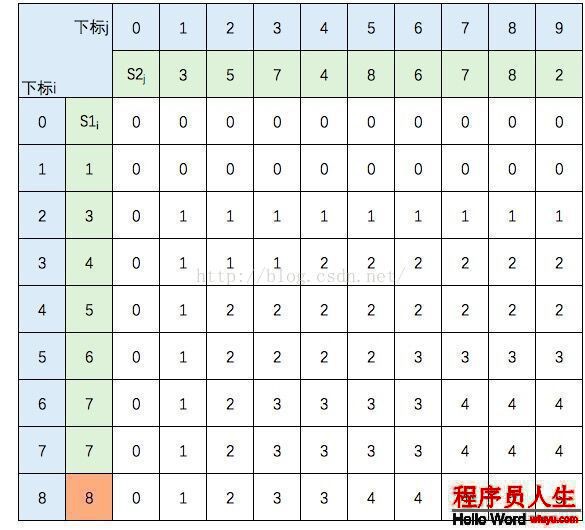
                至此，該表填完。根據性質，c[8,9] = S1 和 S2 的 LCS的長度，即為5。

6.構造LCS

       本文S1和S2的最LCS其實不是只有1個，本文其實不是側重講輸出兩個序列的所有LCS，只是介紹如何通過上表，輸出其中1個LCS。

       我們根據遞歸公式構建了上表，我們將從最后1個元素c[8][9]倒推出S1和S2的LCS。

       c[8][9] = 5，且S1[8] != S2[9]，所以倒推回去，c[8][9]的值來源于c[8][8]的值(由于c[8][8] > c[7][9])。

       c[8][8] = 5,  且S1[8] = S2[8], 所以倒推回去，c[8][8]的值來源于 c[7][7]。

       以此類推，如果遇到S1[i] != S2[j] ，且c[i⑴][j] = c[i][j⑴] 這類存在分支的情況，這里請都選擇1個方向（以后遇到這樣的情況，也選擇相同的方向）。

       第1種結果為：

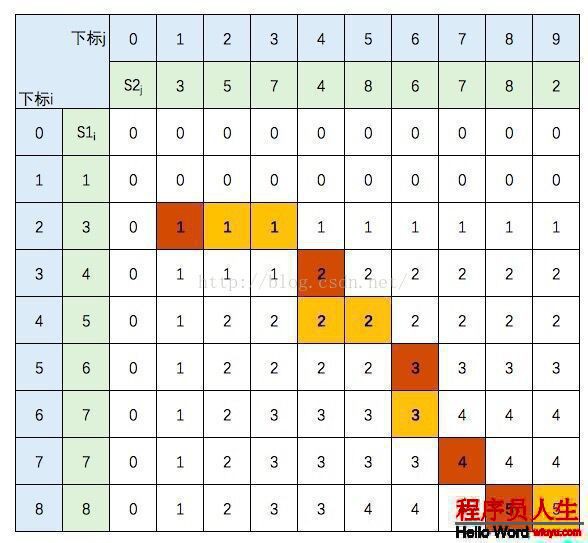
          這就是倒推回去的路徑，棕色方格為相等元素，即LCS = {3,4,6,7,8}，這是其中1個結果。

          如果如果遇到S1[i] != S2[j] ，且c[i⑴][j] = c[i][j⑴] 這類存在分支的情況，選擇另外一個方向，會得到另外一個結果。

           即LCS ={3,5,7,7,8}。

7.關于時間復雜度

        構建c[i][j]表需要Θ(mn)，輸出1個LCS的序列需要Θ(m+n)。

          本文內容參考以下：

        【1】http://baike.baidu.com/link?url=iKrtEZXAQ3LeQLL7Z0HQWpy7EO7BZInUR17C63lAIDFBJ_COm8e3KmKVxQCD6DlOvji2F9W6achz49Z_anZCfa

        【2】《算法導論》第3版 15.4節

        注意：
        如您發現本文檔中有明顯毛病的地方，
        或您發現本文檔中援用了他人的資料而未進行說明時，請聯系我進行更正。
        轉載或使用本文檔時，請作醒目說明。
        必要時請聯系作者，否則將追究相應的法律責任。

        note:
        If you find this document with any error ,
        Or if you find any illegal citations , please contact me correct.
        Reprint or use of this document,Please explain for striking. 
        Please contact the author if necessary, or they will pursue the corresponding legal responsibility.

生活不易，碼農辛苦
如果您覺得本網站對您的學習有所幫助,可以手機掃描二維碼進行捐贈